Category: Uncategorized

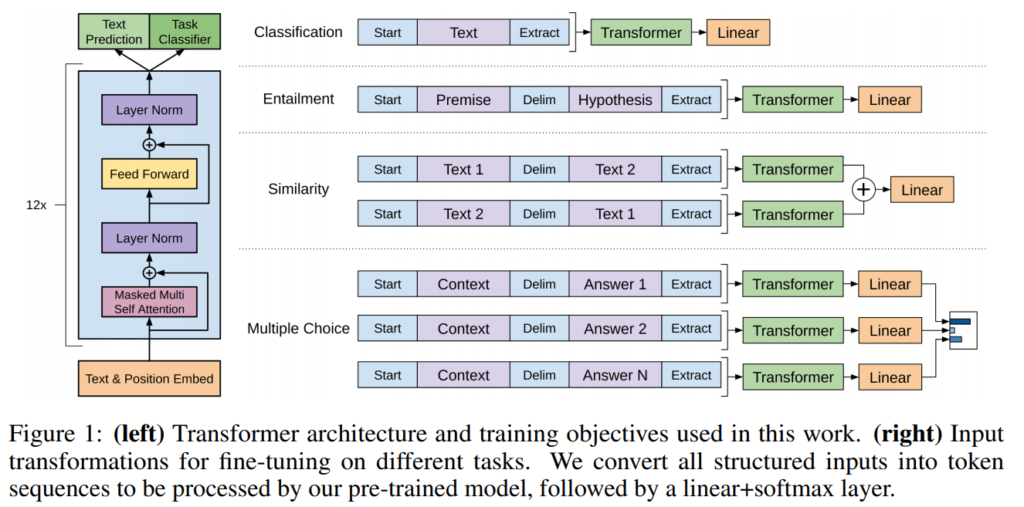
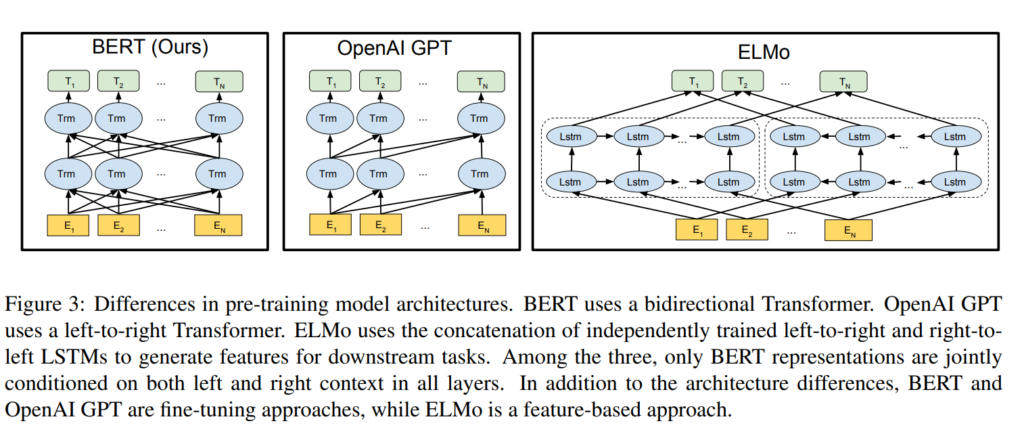
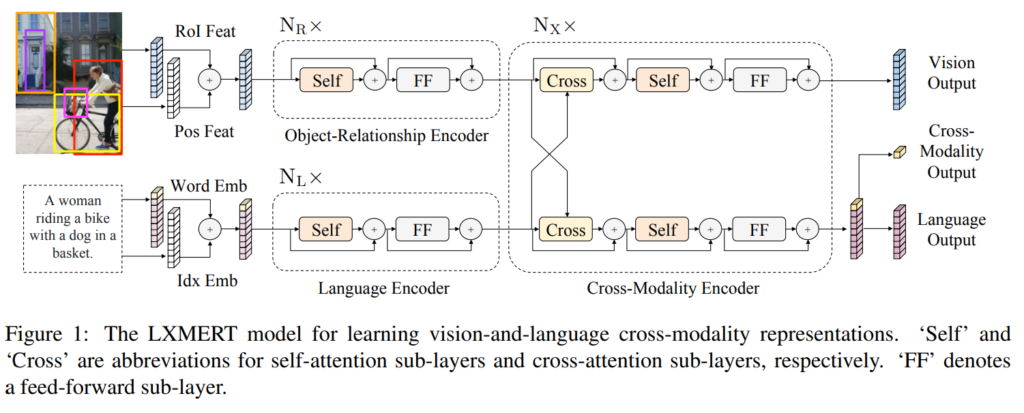
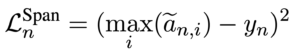I have written short summaries of 68 different research papers published in the areas of Machine Learning and Natural Language Processing. They cover a wide range of different topics, authors and venues. These are not meant to be reviews showing my subjective opinion, but instead I aim to provide a blunt and concise overview of the core contribution of each publication. At the end of the list I have also included a selection of my own papers, published together with my students and collaborators.

Given how many papers are published in our area every year, it is getting more and more difficult to keep track of all of them. The goal of this post is to save some time for both new and experienced readers in the field and allow them to get a quick overview of 68 research papers.

These summaries are written in a way that tries to relay the core idea and main takeaway of the paper without any overhype or marketing wrapper.

It is probably good to also to mention that I wrote all of these summaries myself and they are not generated by any language models.

Here we go.

1. PromptRobust: Towards Evaluating the Robustness of Large Language Models on Adversarial Prompts

Kaijie Zhu, Jindong Wang, Jiaheng Zhou, Zichen Wang, Hao Chen, Yidong Wang, Linyi Yang, Wei Ye, Yue Zhang, Neil Zhenqiang Gong, Xing Xie. Microsoft Research, CAS, CMU, Peking University, Westlake University, Duke University. ArXiv 2023.
https://arxiv.org/abs/2306.04528

The paper investigates LLM robustness to prompt perturbations, measuring how much task performance drops for different models with different attacks. Prompts are changed by introducing spelling errors, replacing synonyms, concatenating irrelevant information or translating from a different language. Word replacement attacks are found to be most effective, with average 33% performance drop. Character-level attacks rank second. GPT-4 and UL2 outperformed other investigated models in terms of robustness.

2. System 2 Attention (is something you might need too)

Jason Weston, Sainbayar Sukhbaatar. Meta. ArXiv 2023.
https://arxiv.org/abs/2311.11829

The paper proposes query rewriting as the solution to the problem of LLMs being overly affected by irrelevant information in the prompts. The first step asks the LLM to rewrite the prompt to remove the irrelevant parts. This edited prompt is then given to the LLM to get the final answer, which improves robustness when the prompts include irrelevant information.

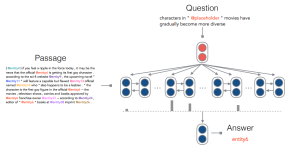
3. Dwell in the Beginning: How Language Models Embed Long Documents for Dense Retrieval

João Coelho, Bruno Martins, João Magalhães, Jamie Callan, Chenyan Xiong. CMU, University of Lisbon, NOVA School of Science and Technology. ArXiv 2024.
https://arxiv.org/abs/2404.04163

The paper investigates positional biases when encoding long documents into a vector for similarity-based retrieval. They start with a pre-trained T5-based model and show that this by itself isn’t biased. However, when using contrastive training (either unsupervised or supervised) to optimize the model for retrieval, the model starts to perform much better when the evidence is in the beginning of the text. They find evidence to indicate that this bias is part of the task itself – important information tends to be towards the beginning of the texts, so that is where the models learns to look more.

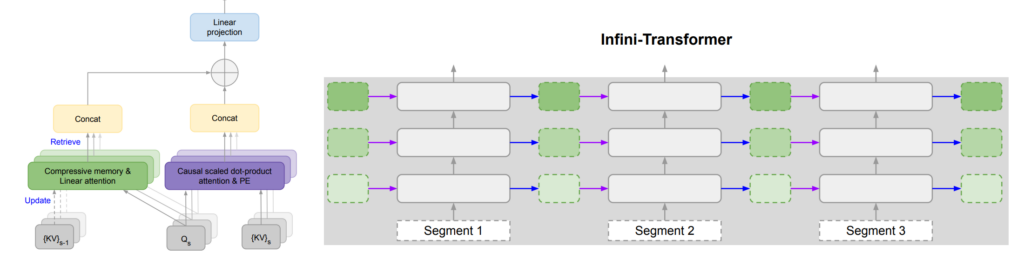
4. Leave No Context Behind: Efficient Infinite Context Transformers with Infini-attention

Tsendsuren Munkhdalai, Manaal Faruqui, Siddharth Gopal. Google. ArXiv 2024.
https://arxiv.org/abs/2404.07143

The paper extends the attention in transformers (which have inefficient quadratic complexity) with a memory component that considerably increases the effective context length. The memory approximates a key-value store by recursively adding previous values into a matrix of parameters as the model moves through context. They show state-of-the-art results on long-context language modelling, finding a hidden passcode from a 1M token length context, and summarizing 500K length books.

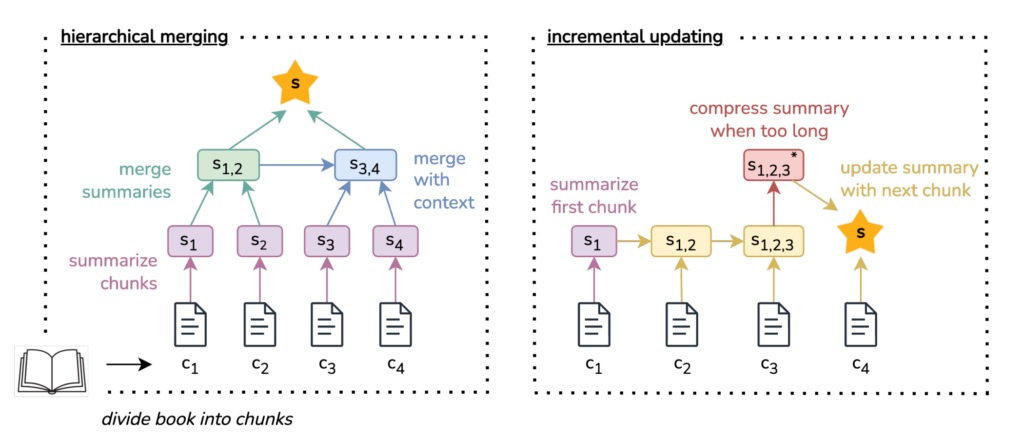
5. BooookScore: A systematic exploration of book-length summarization in the era of LLMs

Yapei Chang, Kyle Lo, Tanya Goyal, Mohit Iyyer. UMass Amherst, AllenAI, Princeton. ICLR 2024.
https://arxiv.org/abs/2310.00785

The paper investigates two strategies for LLM evaluation of reading full-length books: hierarchically combining chunk-level summaries and incrementally building up a summary while going through the book. They focus on coherence, as opposed to correctness, and develop an automated LLM-based score (BooookScore) for assessing summaries. They first have humans assess each sentence of a sample of generated summaries, then check that the automated metric correlates with the human assessment. The results indicate that hierarchical summarisation produces more coherent summaries while incremental summarisation leads to more details being retained in the summary.

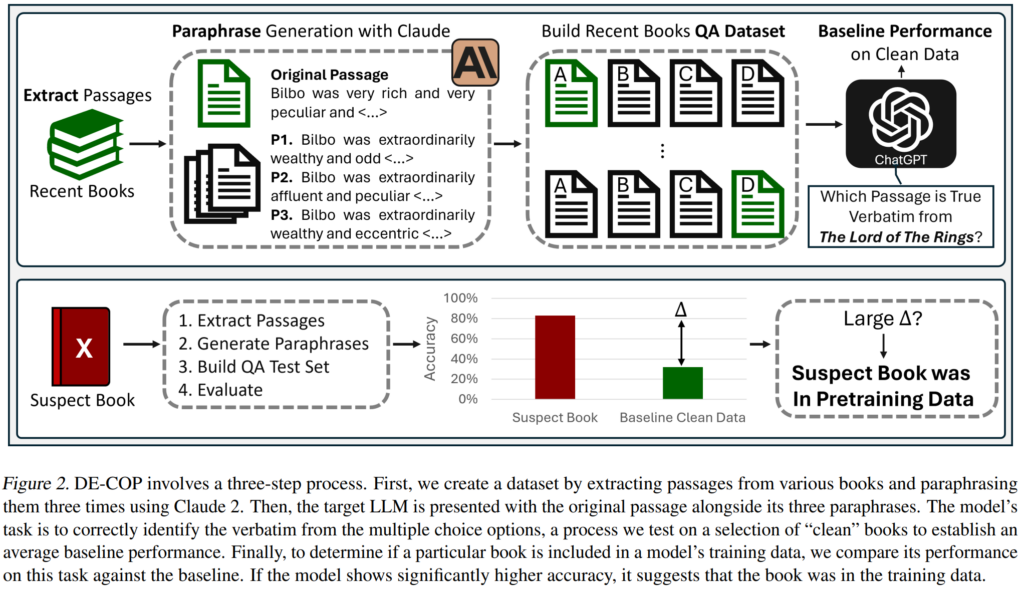
6. DE-COP: Detecting Copyrighted Content in Language Models Training Data

André V. Duarte, Xuandong Zhao, Arlindo L. Oliveira, Lei Li. ULisboa, UCSB, CMU. ICML 2024.
https://arxiv.org/abs/2402.09910

The paper proposes a simple approach to determining whether a particular book has been used for training an LLM. A paragraph from the book is presented to the model, along with multiple paraphrases. The model is then asked to choose which paragraph came from the book. The results are surprisingly good, improving over baselines using probabilities and perplexities.

7. STaR-GATE: Teaching Language Models to Ask Clarifying Questions

Chinmaya Andukuri, Jan-Philipp Fränken, Tobias Gerstenberg, Noah D. Goodman. Stanford. ArXiv 2024.
https://arxiv.org/abs/2403.19154

The paper focuses on teaching LLMs to ask clarifying questions instead of trying to immediately answer user questions and instructions in one turn. They set up two LLMs to chat with each other – the Roleplayer has a secret persona and asks a scripted question, while the Questioner is tasked with answering the question after asking clarifying questions. They sample alternative dialogue traces, identify the one that led to the best final answer, then supervise the Questioner with this best dialogue. The results show that the trained Questioner is able to provide better persona-specific answers.

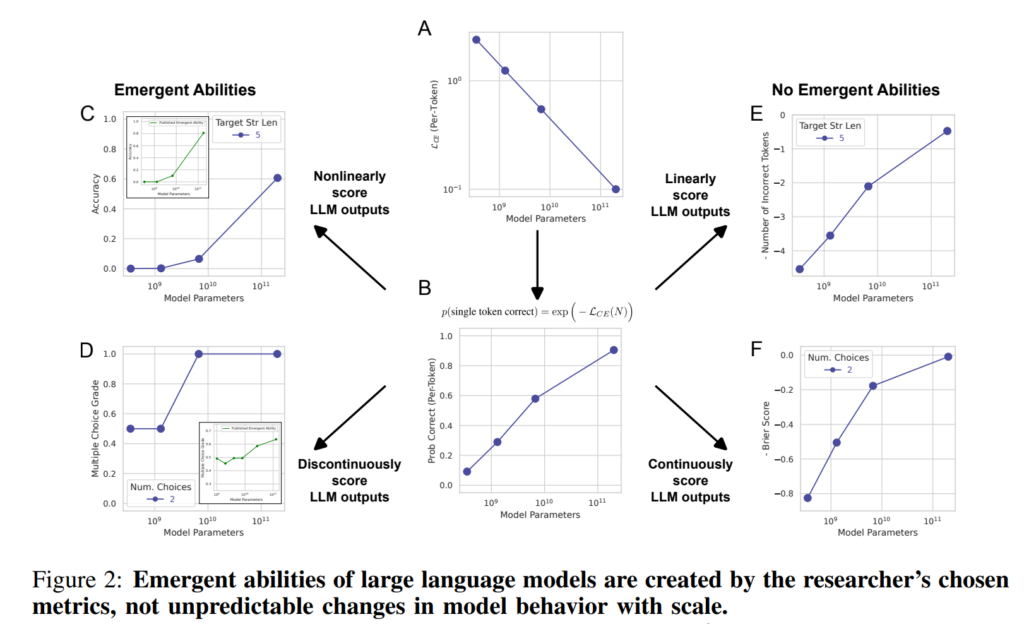
8. Are Emergent Abilities of Large Language Models a Mirage?

Rylan Schaeffer, Brando Miranda, Sanmi Koyejo. Stanford. NeurIPS 2023.
https://arxiv.org/abs/2304.15004

This paper questions the claim that LLMs have emergent abilities – unexpected skills that suddenly appear only with models that are sufficiently large. They show that this property is mostly due to the use of discontinuous metrics, which only credit models once they reach sufficiently high levels of abilities. When using smooth continuous metrics, and increasing test sets to sufficient size, the “sudden appearance” of abilities is replaced by gradual improvements.

9. Distinguishing the Knowable from the Unknowable with Language Models

Gustaf Ahdritz, Tian Qin, Nikhil Vyas, Boaz Barak, Benjamin L. Edelman. Harvard. ICML 2024.
https://arxiv.org/abs/2402.03563

The paper investigates the possibility of distinguishing epistemic uncertainty (due to lack of knowledge) from aleatoric uncertainty (due to entropy in the underlying distribution) in LLMs. They make the assumption that a large LLM has no (or less) epistemic uncertainty and train a probe to predict the uncertainty of a large LLM based on the frozen activations of a smaller LLM. This is largely successful, indicating that the model activations in the smaller model are able to differentiate between the different uncertainty types. They also propose that in-context information affects the LLM probabilities more in the case of epistemic uncertainty, and less with aleatoric uncertainty.

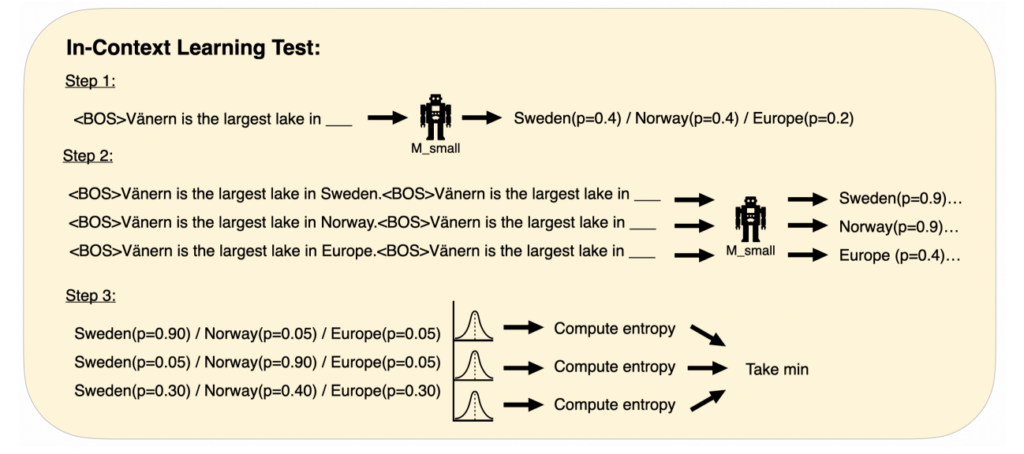
10. Do Large Language Models Latently Perform Multi-Hop Reasoning?

Sohee Yang, Elena Gribovskaya, Nora Kassner, Mor Geva, Sebastian Riedel. DeepMind, UCL, Google Research, Tel Aviv University. ArXiv 2024.
https://arxiv.org/abs/2402.16837

The paper investigates the ability of LLMs to perform latent multi-hop reasoning, by completing sentences such as “The author of the novel Ubik was born in the city of …”. They construct experiments to investigate each hop separately: 1) whether the internal representation for the intermediate entity (“Philip K. Dick”) required for the first hop strengthens, and 2) whether increased recall of the intermediate entity improves the consistency of the final answer. In these experiments they find strong evidence for the first hop and moderate evidence for the second hop. They construct a dataset of 45,595 pairs of one-hop and two-hop prompts, to be released.

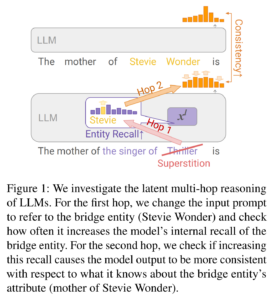
11. PhaseEvo: Towards Unified In-Context Prompt Optimization for Large Language Models

Wendi Cui, Jiaxin Zhang, Zhuohang Li, Hao Sun, Damien Lopez, Kamalika Das, Bradley Malin, Sricharan Kumar. Intuit, Vanderbilt, Cambridge. ArXiv 2024.
https://arxiv.org/abs/2402.11347

The paper describes an evolution strategy for finding optimal LLM prompts for specific tasks. Prompts are first initialised either by experts or by asking an LLM to recover the prompt based on example input-output pairs. These initial prompts then go through multiple mutation steps, by having the LLM rewrite the prompts according to different strategies. The fitness of the prompts is measured by performance on the dev set and the best prompt is then evaluated on the test set.

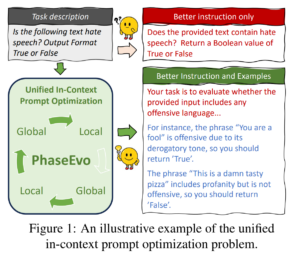
12. Can LLMs Reason with Rules? Logic Scaffolding for Stress-Testing and Improving LLMs

Siyuan Wang, Zhongyu Wei, Yejin Choi, Xiang Ren. Fudan University, University of Washington, USC, AllenAI. ArXiv 2024.
https://arxiv.org/abs/2402.11442

The paper first constructs a dataset of 14000 commonsense logical rules, using LLMs to generate and check the rules. They then assess LLM understanding of these rules by turning the rules into a binary entailment classification task, showing that all models decrease in performance as the complexity of the rules increases. Finally, they train an LLM with these rules and show benefit on downstream tasks that require commonsense reasoning.

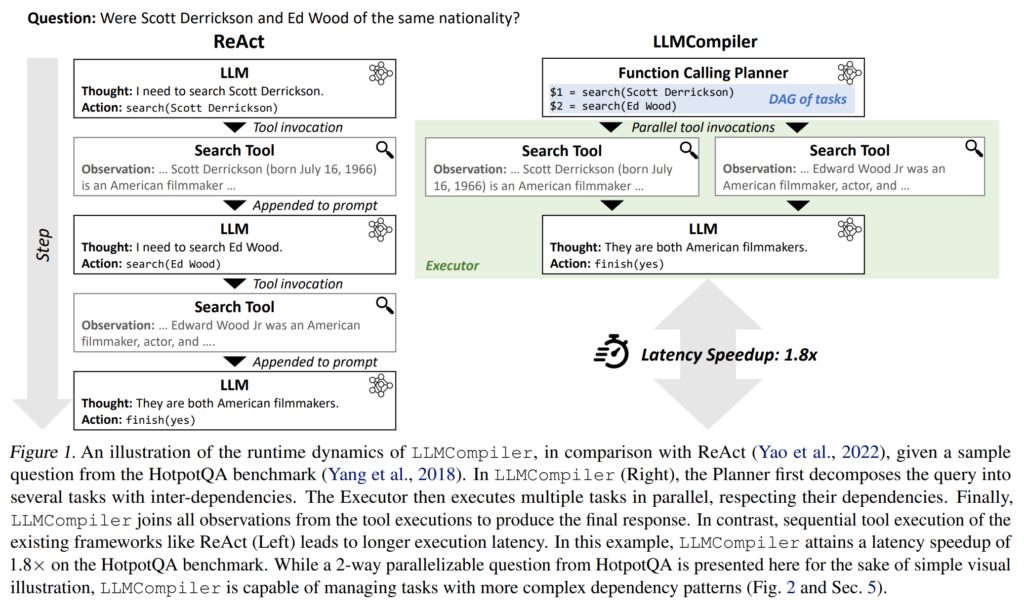
13. An LLM Compiler for Parallel Function Calling

Sehoon Kim, Suhong Moon, Ryan Tabrizi, Nicholas Lee, Michael W. Mahoney, Kurt Keutzer, Amir Gholami. UC BErkeley, ICSI, LBNL. ICML 2024.
https://arxiv.org/abs/2312.04511

While most LLMs perform tool calls sequentially, in a linear iteration loop, this paper investigates executing tool calls in parallel. The planner stage first predicts which tool calls will be needed and what are the dependencies between the tool calls. These tools are then called in parallel and the results are then combined for the final answer. They show performance improvements in some settings and speed improvements in all evaluated settings, showing particular usefulness in settings where the LLM needs to retrieve information about multiple entities (e.g. do background research) in order to reach the final solution.

14. Interpreting Language Models with Contrastive Explanations

Kayo Yin, Graham Neubig. UC Berkeley, CMU. EMNLP 2022.
https://aclanthology.org/2022.emnlp-main.14/

Proposes an explainability method for language modelling that explains why one word was predicted instead of a specific other word. Adapts three different explainability methods to this contrastive approach and evaluates on a dataset of minimally different sentences. The method is shown to better highlight the differences between these specific words, instead of just assigning most of the focus to the previous word.

15. Crossmodal-3600: A Massively Multilingual Multimodal Evaluation Dataset

Ashish V. Thapliyal, Jordi Pont-Tuset, Xi Chen, Radu Soricut. Google Research. EMNLP 2022.
https://arxiv.org/abs/2205.12522

Multilingual image captioning dataset containing captions in 36 languages for 3600 images. An annotation process has been designed to make sure all the annotations resemble the same style, similar to an automated captioning output. Results show that the dataset provides a much higher correlation to human judgements, compared to the silver annotations from COCO-dev.

16. Locating and Editing Factual Associations in GPT

Kevin Meng, David Bau, Alex Andonian, Yonatan Belinkov. MIT, Northeastern, Technion IIT. NeurIPS 2022.
https://arxiv.org/abs/2202.05262

Proposes a method for editing a specific relational fact in a pre-trained language model. The specific feedforward layer that is responsible for recalling the target of a specific fact is identified using noisy permutations of the model activations. The feedforward layer is then directly trained to produce a more optimal output when given the subject of that fact as input.

17. M2D2: A Massively Multi-Domain Language Modeling Dataset

Machel Reid, Victor Zhong, Suchin Gururangan, Luke Zettlemoyer. The University of Tokyo, University of Washington. EMNLP 2022.
https://aclanthology.org/2022.emnlp-main.63/

Assembling a dataset for language model domain adaptation, from Wikipedia and ArXiv, containing 22 broad domains and 145 fine-grained domains. Experiments show that when fine-tuning a model for in-domain data, it is best to tune on related broad domain data first, then further only on the specific fine-grained domain data. Out-of-domain performance is shown to strongly correlate with vocabulary overlap between the different domains.

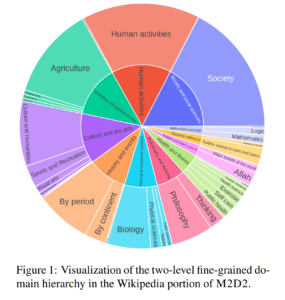
18. Binding Language Models in Symbolic Languages

Zhoujun Cheng, Tianbao Xie, Peng Shi, Chengzu Li, Rahul Nadkarni, Yushi Hu, Caiming Xiong, Dragomir Radev, Mari Ostendorf, Luke Zettlemoyer, Noah A. Smith, Tao Yu. The University of Hong Kong, Shanghai Jiao Tong University, University of Washington, AllenAI, University of Waterloo, Salesforce Research, Yale University, Meta AI. ICLR 2023.
https://arxiv.org/abs/2210.02875

Uses a large pre-trained language model (GPT-3 Codex) to translate a natural language question into an SQL query. This query can then contain API calls, which also get executed by the language model, in order to populate additional columns of information in a database, over which the SQL can then operate. Outperforms previous methods on datasets of questions about data tables, using only contextual examples without fine-tuning the language model.

19. Hungry Hungry Hippos: Towards Language Modeling with State Space Models

Daniel Y. Fu, Tri Dao, Khaled K. Saab, Armin W. Thomas, Atri Rudra, Christopher Ré. Stanford, University at Buffalo. ICLR 2023.
https://arxiv.org/abs/2212.14052

Proposes a modification for state space models, a version of RNN with linear operations that can be separated into components of cumulative sums. The modification gives them abilities similar to attention, being able to copy and compare tokens across the sequence. The architecture scales O(N log N) with sequence length N, as opposed to N^2 for regular attention.

20. Why Can GPT Learn In-Context? Language Models Implicitly Perform Gradient Descent as Meta-Optimizers

Damai Dai, Yutao Sun, Li Dong, Yaru Hao, Shuming Ma, Zhifang Sui, Furu Wei. ACL 2023.
https://aclanthology.org/2023.findings-acl.247/

Shows how the equations for attention during in-context learning (showing the model examples in the input) can be thought of as a form of gradient descent. Experiments indicate that there are also similarities in how these methods affect the model in practice.

21. PAL: Program-aided Language Models

Luyu Gao, Aman Madaan, Shuyan Zhou, Uri Alon, Pengfei Liu, Yiming Yang, Jamie Callan, Graham Neubig. CMU, Inspired Cognition. ICML 2023.
https://arxiv.org/abs/2211.10435

Question answering with a language model while generating a chain-of-thought, outputting the necessary reasoning steps to get to the answer. In addition to natural language reasoning steps, the model generates python syntax that is then executed in order to output the final answer. This is shown to improve results, particularly when the result requires mathematical arithmetic over large numbers.

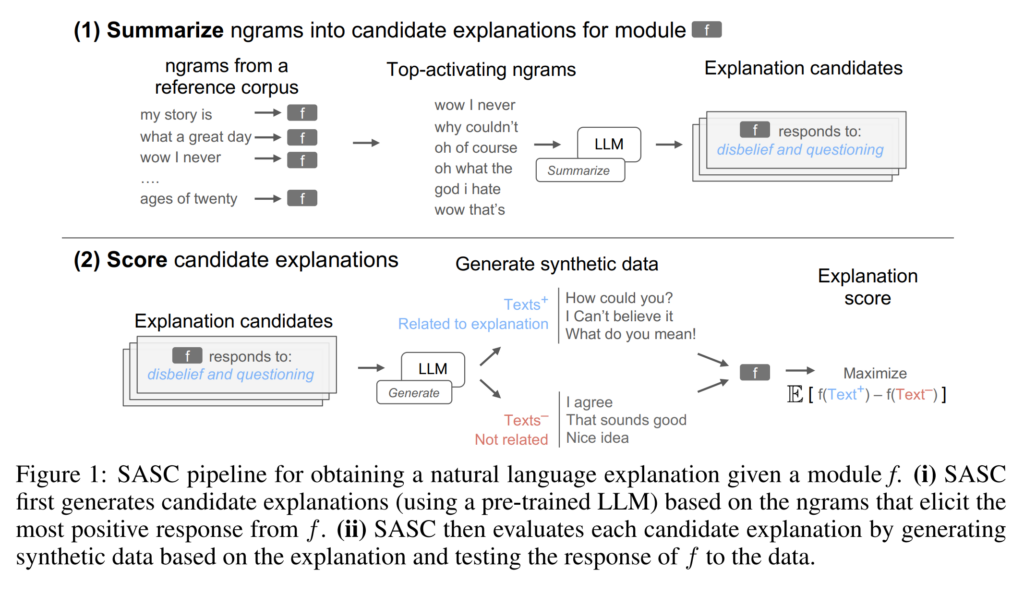
22. Explaining black box text modules in natural language with language models

Chandan Singh, Aliyah R. Hsu, Richard Antonello, Shailee Jain, Alexander G. Huth, Bin Yu, Jianfeng Gao. MSR, UC Berkeley, UT Austin. NeurIPS XAIA 2023.
https://arxiv.org/abs/2305.09863

A method for providing natural language explanations to black-box modules that take neurons as input and return a score as output. A large number of ngrams are passed through the model in order to identify ngrams that result in the largest score. These ngrams are sampled and fed into an LLM for summarization, generating explanation candidates. An LLM is then used for generating positive and negative example sentences based on each candidate explanation, and the score differences between these examples are used for selecting the best explanation.

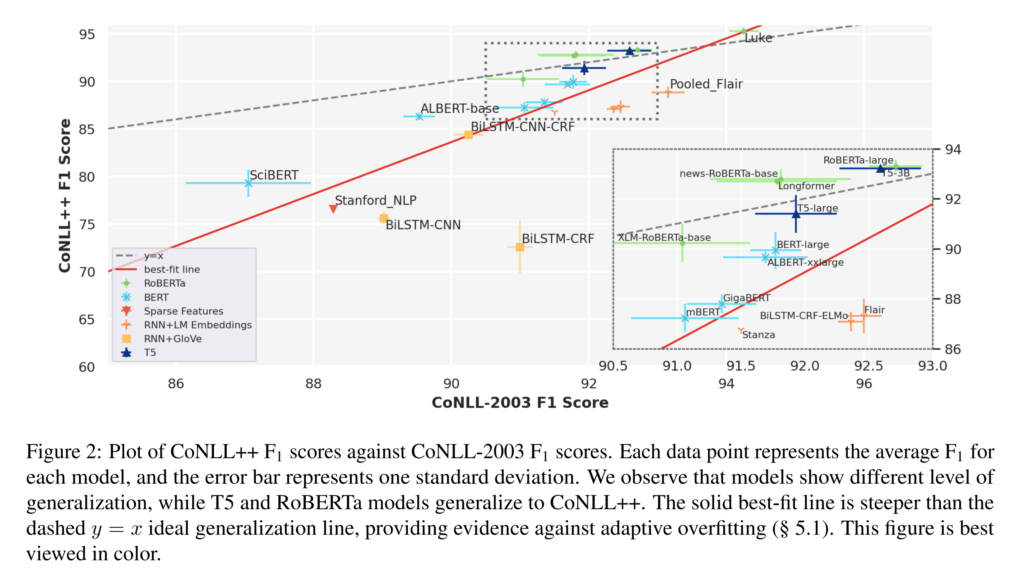
23. Do CoNLL-2003 Named Entity Taggers Still Work Well in 2023?

Shuheng Liu, Alan Ritter. Georgia Institute of Technology. ACL 2023.
https://arxiv.org/abs/2212.09747

A thorough investigation of well-known NER models and how their performance is affected on modern data when trained on CoNLL 2003. They annotate a new test set of news data from 2020 and find that performance of certain models holds up very well and the field luckily hasn’t overfitted to the CoNLL 2003 test set. For best results on modern data, large models pre-trained on contemporary corpora come out on top, with RoBERTa, T5 and LUKE standing out.

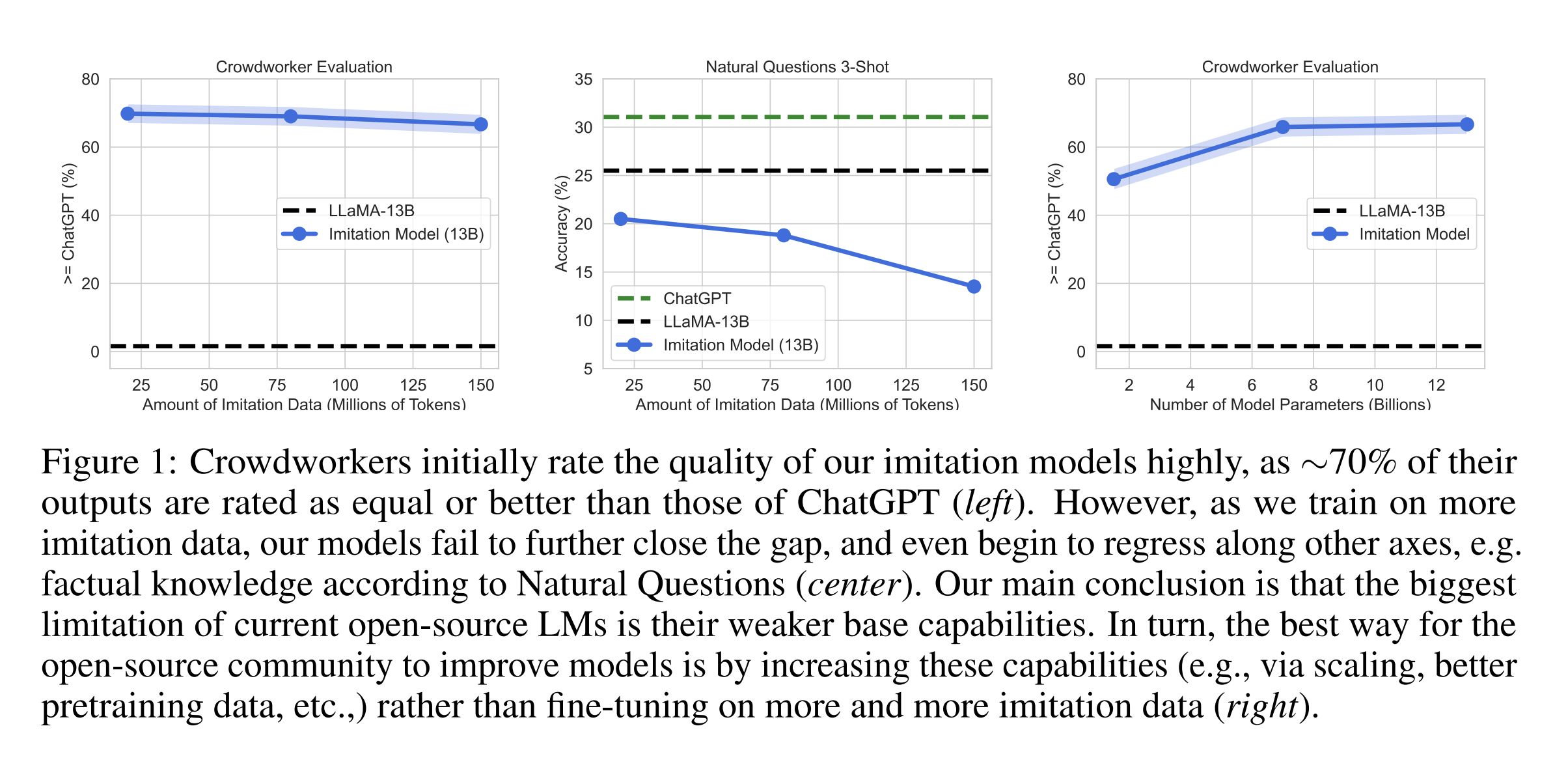
24. The False Promise of Imitating Proprietary LLMs

Arnav Gudibande, Eric Wallace, Charlie Snell, Xinyang Geng, Hao Liu, Pieter Abbeel, Sergey Levine, Dawn Song. UC Berkeley. ArXiv 2023.
https://arxiv.org/abs/2305.15717

Analyzing the performance of open-source LLMs fine-tuned on the outputs of proprietary LLMs. They conclude that when fine-tuned on general-purpose dialogues, the models learn to mimic the style of the teacher model and can fool human assessors, but lack core knowledge and can more easily generate factually incorrect claims. However, when fine-tuning only for a specific task, then this imitation strategy can reach near-parity with the teacher models.

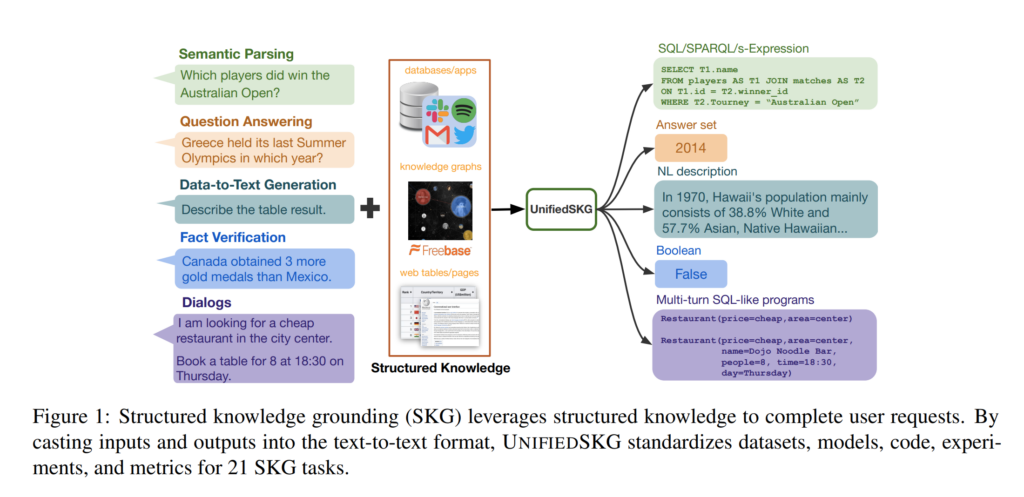
25. UnifiedSKG: Unifying and Multi-Tasking Structured Knowledge Grounding with Text-to-Text Language Models

Tianbao Xie, Chen Henry Wu, Peng Shi, Ruiqi Zhong, Torsten Scholak, Michihiro Yasunaga, Chien-Sheng Wu, Ming Zhong, Pengcheng Yin, Sida I. Wang, Victor Zhong, Bailin Wang, Chengzu Li, Connor Boyle, Ansong Ni, Ziyu Yao, Dragomir Radev, Caiming Xiong, Lingpeng Kong, Rui Zhang, Noah A. Smith, Luke Zettlemoyer, Tao Yu. Misc. EMNLP 2022.
https://aclanthology.org/2022.emnlp-main.39

Unifies 21 generation tasks that require accessing structured information sources into a general sequence-to-sequence benchmark for language models. It includes datasets on semantic parsing, question answering, data-to-text, dialogue and fact verification. The input, structured data and and output is linearised for these datasets, so that a general-purpose language model can be used for all of them. A fine-tuned T5 model is shown to outperform existing SOTA models on many of these datasets.

26. Toolformer: Language Models Can Teach Themselves to Use Tools

Timo Schick, Jane Dwivedi-Yu, Roberto Dessì, Roberta Raileanu, Maria Lomeli, Luke Zettlemoyer, Nicola Cancedda, Thomas Scialom. Meta, Universitat Pompeu Fabra. NeurIPS 2023.
https://openreview.net/forum?id=Yacmpz84TH

The paper describes a method for teaching large language models to use external tools. A supervised dataset is created by trying to insert results from API calls into various points in the text, then only retaining the cases where doing that improves perplexity. The LM is then fine-tuned on this dataset and manages to improve performance on several tasks by using tools such as a QA system, Wikipedia search and a calculator.

27. ToolkenGPT: Augmenting Frozen Language Models with Massive Tools via Tool Embeddings

Shibo Hao, Tianyang Liu, Zhen Wang, Zhiting Hu. UC San Diego, Mohamed bin Zayed University of Artificial Intelligence. NeurIPS 2023.
https://openreview.net/forum?id=BHXsb69bSx

The paper presents ToolkenGPT, a framework for extending LMs with tool use. For each new tool, a new token is added to the output vocabulary of the LM and the embedding for that token is trained with annotated or synthetic examples. When the LM generates that token, the model is switched to a different mode and prompted with examples for that particular tool in order to generate the necessary arguments for that tool call. 

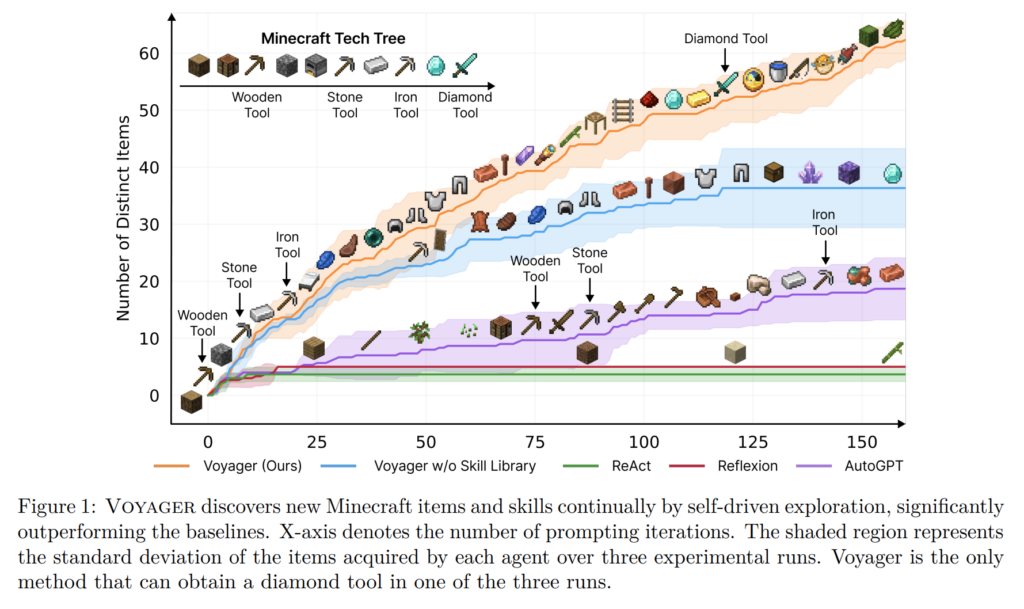
28. Voyager: An Open-Ended Embodied Agent with Large Language Models

Guanzhi Wang, Yuqi Xie, Yunfan Jiang, Ajay Mandlekar, Chaowei Xiao, Yuke Zhu, Linxi Fan, Anima Anandkumar. NVIDIA, Caltech, UT Austin, Stanford, UW Madison. TMLR 2024.
https://arxiv.org/abs/2305.16291

Combining together black-box LLMs through different prompting strategies to create a capable agent for playing Minecraft. One component receives information about the current state, reasons about the next possible goals and formulates a suitable task in natural language. Another component receives the desired task along with descriptions of existing API functions and skills, then iteratively generates and improves a code function for performing that task.

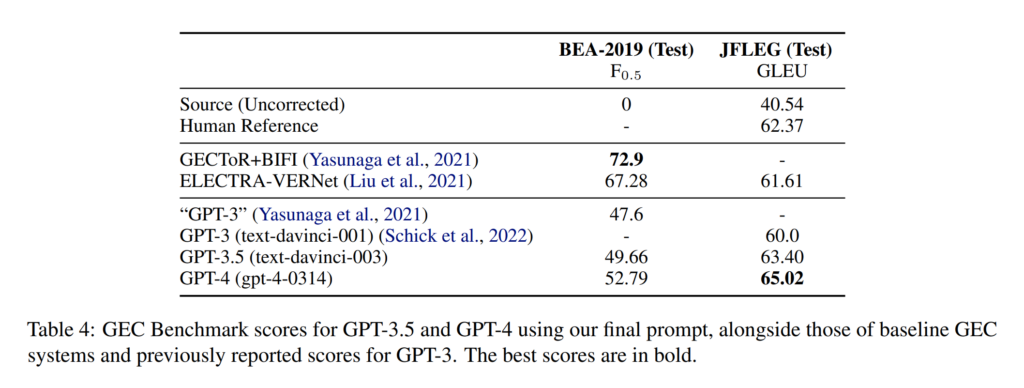
29. Analyzing the Performance of GPT-3.5 and GPT-4 in Grammatical Error Correction

Steven Coyne, Keisuke Sakaguchi, Diana Galvan-Sosa, Michael Zock, Kentaro Inui. Tohoku University, RIKEN, Aix-Marseille University. ArXiv 2023.
https://arxiv.org/abs/2303.14342

Evaluating well-known LLMs on two established benchmarks for grammatical error correction (GEC). They find that specific prompts matter quite a bit and lower temperature is better for GEC. The results show that LLMs tend to over-correct and perform fluency edits, achieving state-of-the-art performance on a dataset designed for this type of edits (JFLEG). However, performance is considerably lower on a benchmark that focuses on minimal edits and only fixing grammaticality (BEA-2019).

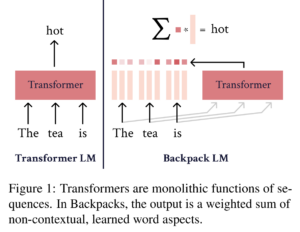
30. Backpack Language Models

John Hewitt, John Thickstun, Christopher D. Manning, Percy Liang. Stanford. ACL 2023.
https://aclanthology.org/2023.acl-long.506

Proposes a language model architecture that maps each word to multiple sense vectors, uses a separate model to predict the weights for these senses, then directly outputs a prediction as a log-linear function. Experiments show that performance degrades, as many more parameters are required to reach a perplexity comparable to a transformer LM. They find that editing the weights of these sense vectors can be used for mitigating gender bias or editing specific information.

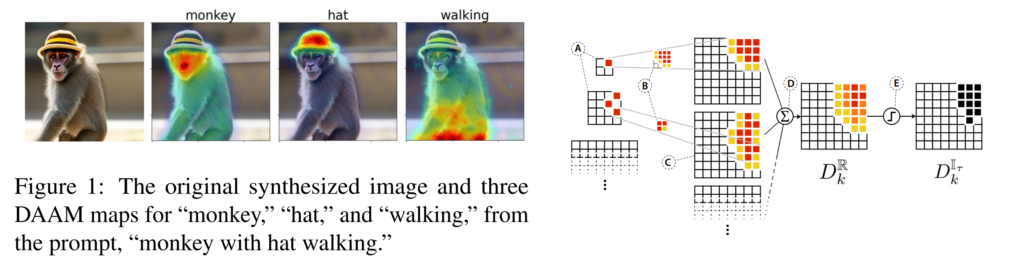
31. What the DAAM: Interpreting Stable Diffusion Using Cross Attention

Raphael Tang, Linqing Liu, Akshat Pandey, Zhiying Jiang, Gefei Yang, Karun Kumar, Pontus Stenetorp, Jimmy Lin, Ferhan Ture. Comcast Applied AI, UCL, University of Waterloo. ACL 2023.
https://aclanthology.org/2023.acl-long.310

A method for analysing text-to-image models, indicating which areas of the generated image are attributed to a particular word in the input. They use the attention scores in Stable Diffusion between convolutional blocks and word embeddings, upscaling and aggregating them between different heads, layers and time steps. The result is competitive to supervised image segmentation models and they use it for linguistic analysis. For example, they show that cohyponyms (e.g. a giraffe and a zebra) in the input can have their concepts merged, resulting in only one of the objects being generated.

32. ToolLLM: Facilitating Large Language Models to Master 16000+ Real-world APIs

Yujia Qin, Shihao Liang, Yining Ye, Kunlun Zhu, Lan Yan, Yaxi Lu, Yankai Lin, Xin Cong, Xiangru Tang, Bill Qian, Sihan Zhao, Lauren Hong, Runchu Tian, Ruobing Xie, Jie Zhou, Mark Gerstein, Dahai Li, Zhiyuan Liu, Maosong Sun. Tsinghua University, ModelBest, Renmin University of China, Yale University, WeChat AI, Tencent, Zhihu. ICLR 2024.
https://arxiv.org/abs/2307.16789

They crawl documentation for 16K APIs from RapidAPI and synthesize an instruction tuning dataset for using these APIs.
Instruction examples are generated using ChatGPT, by asking it to generate examples that make use of one or multiple sample APIs.
Multiple rounds of API calls and responses are allowed by the LLM, which are explored using a depth-first search strategy, until a final answer or termination is generated.

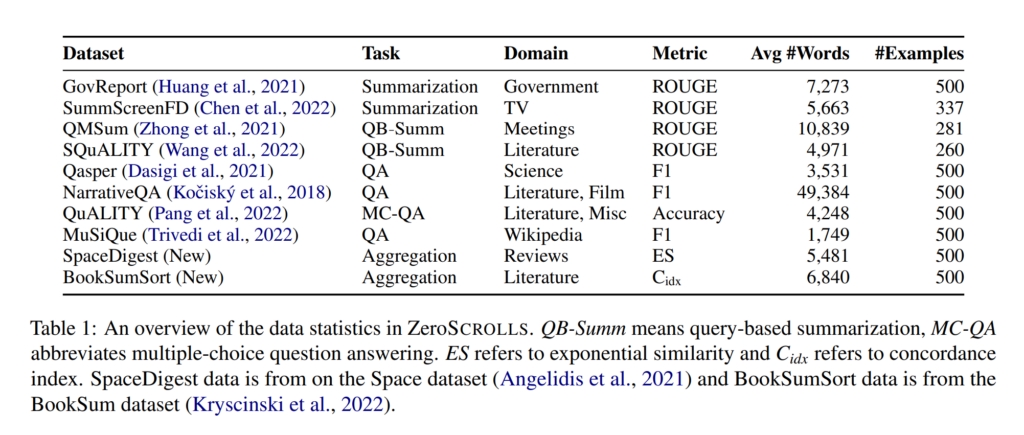
33. ZeroSCROLLS: A Zero-Shot Benchmark for Long Text Understanding

Uri Shaham, Maor Ivgi, Avia Efrat, Jonathan Berant, Omer Levy. Tel Aviv University, Meta AI. EMNLP 2023.
https://aclanthology.org/2023.findings-emnlp.536

Constructing a benchmark for zero-shot understanding of long texts with LLMs. Includes existing datasets (summarization, QA) from the Scrolls benchmark, along with two new tasks: determining the ratio of positive reviews in a set of reviews, and sorting a shuffled list of book chapter summaries. Results indicate that GPT-4 is best overall, even though it loses points in automatic evaluation as it doesn’t follow the instructed format.

34. Parameter-Efficient Instruction Tuning of Large Language Models For Extreme Financial Numeral Labelling

Subhendu Khatuya, Rajdeep Mukherjee, Akash Ghosh, Manjunath Hegde, Koustuv Dasgupta, Niloy Ganguly, Saptarshi Ghosh, Pawan Goyal. Indian Institute of Technology Kharagpur, Goldman Sachs. NAACL 2024.
https://aclanthology.org/2024.naacl-long.410/

The paper approaches the task of tagging entities with a large number of labels using a generative model. The LLM is instruction-tuned to generate the label description of the label. The generated description is then mapped to the closest real label description using sentence embeddings and cosine similarity. The method achieves strong performance over other traditional tagging models on this task.

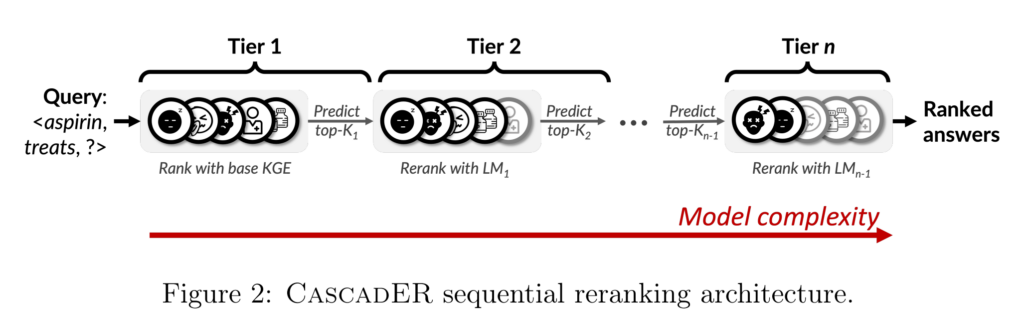
35. CascadER: Cross-Modal Cascading for Knowledge Graph Link Prediction

Tara Safavi, Doug Downey, Tom Hope. University of Michigan, Allen Institute for Artificial Intelligence, Northwestern University, The Hebrew University of Jerusalem. AKBC 2022.
https://arxiv.org/abs/2205.08012

Proposes a pipeline of increasingly complex models for predicting links in graph. Simpler models are used to perform initial filtering, then more complex models that need much processing time are applied only on a small chosen sample. The number of candidates to retain at each stage is learned in a supervised way. The model makes it feasible to apply very large models to large tasks while also improving the SOTA results.

36. Revisiting Transformer-based Models for Long Document Classification

Xiang Dai, Ilias Chalkidis, Sune Darkner, Desmond Elliott. CSIRO Data61, University of Copenhagen. EMNLP 2022.
https://aclanthology.org/2022.findings-emnlp.534.pdf

Comparing sparse attention (Longformer) and hierarchical transformers for long document classification, focusing on electronic health records. They find that the performance is close, with Longformer slightly better out-of-the-box and hierarchical models better after tuning hyperparameters. Results also indicate that splitting long text into overlapping sections and using Label-Wise Attention Network helps improve performance.

37. Socratic Models: Composing Zero-Shot Multimodal Reasoning with Language

Andy Zeng, Maria Attarian, Brian Ichter, Krzysztof Choromanski, Adrian Wong, Stefan Welker, Federico Tombari, Aveek Purohit, Michael Ryoo, Vikas Sindhwani, Johnny Lee, Vincent Vanhoucke, Pete Florence. Google. ICLR 2023.
https://arxiv.org/abs/2204.00598

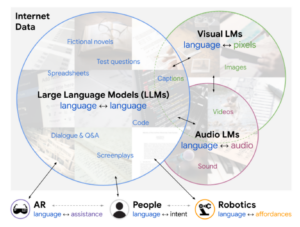
Constructs a pipeline of pre-trained language models with different modalities for scene understanding. Visual LMs rank possible locations and objects, audio LMs rank possible sounds, regular LMs take this information in a filled-out template and generate summaries or answers for QA. LMs can also be used to generate candidate activities, based on the detected places and objects, then these activities are re-ranked by a visual LM to choose ones that match the scene.

38. LIFT: Language-Interfaced Fine-Tuning for Non-Language Machine Learning Tasks

Tuan Dinh, Yuchen Zeng, Ruisu Zhang, Ziqian Lin, Michael Gira, Shashank Rajput, Jy-yong Sohn, Dimitris Papailiopoulos, Kangwook Lee. University of Wisconsin-Madison. NeurIPS 2022.
https://arxiv.org/abs/2206.06565

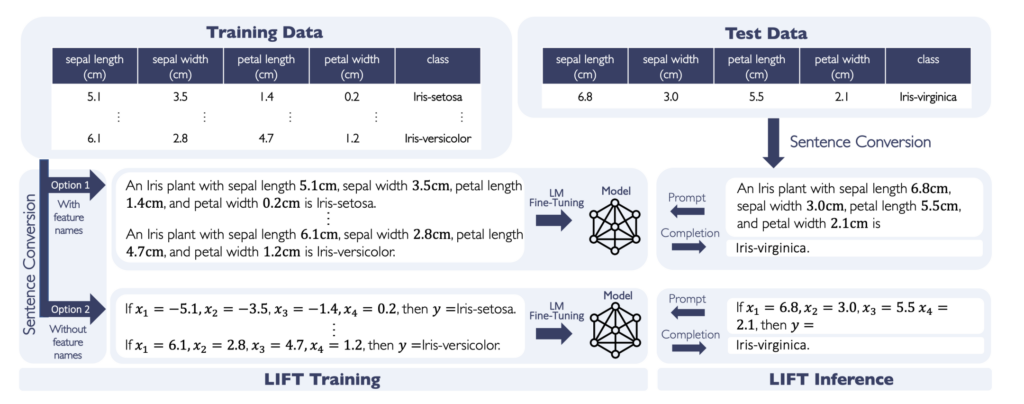
The paper investiagtes the application of pre-trained language models on the task of classifying non-textual data, without any architecture changes.
The input features are linearized into a text-like sequence and given as context, the output is then collected as a language model prediction.
While it doesn’g perform best overall, it does achieve surprisingly competitive performance.

39. Few-Shot Tabular Data Enrichment Using Fine-Tuned Transformer Architectures

Asaf Harari, Gilad Katz. Ben-Gurion University of the Negev. ACL 2022.
https://aclanthology.org/2022.acl-long.111.pdf

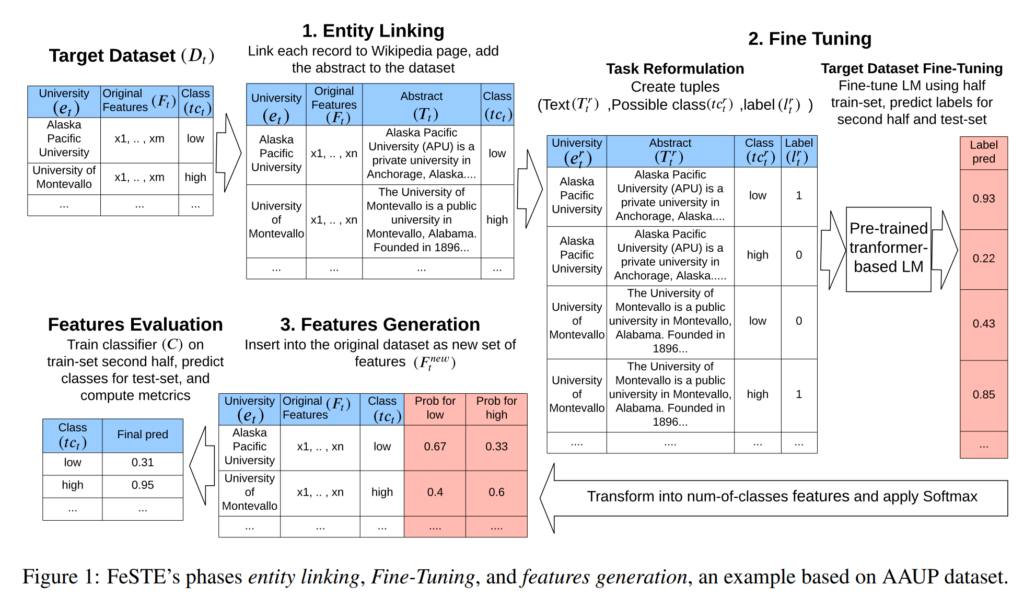
System for creating additional feature columns for a tabular dataset, which can then be useful for classification. Entities (rows) in the data are matched to wikipedia articles in order to retrieve plain text descriptions. Binary classifiers are then trained to classify this text according to properties from the tabular data, and the output probabilities are included as new features in the dataset. Evaluation is performed on the main classification task by using these new extra features.

40. Counterfactual Memorization in Neural Language Models

Chiyuan Zhang, Daphne Ippolito, Katherine Lee, Matthew Jagielski, Florian Tramèr, Nicholas Carlini. Google Research, Carnegie Mellon University, Google DeepMind, ETH Zürich. NeurIPS 2023.
https://arxiv.org/abs/2112.12938

The paper proposes a measure of counterfactual memorization for pre-trained language models.
A large number of different models are trained on subsets of the training set.
The expected performance on that sentence is then calculated for examples containing a particular sentence, versus those that do not contain this sentence.
A high score difference indicates that the model tends to memorize this sentence when it is included in the training data.

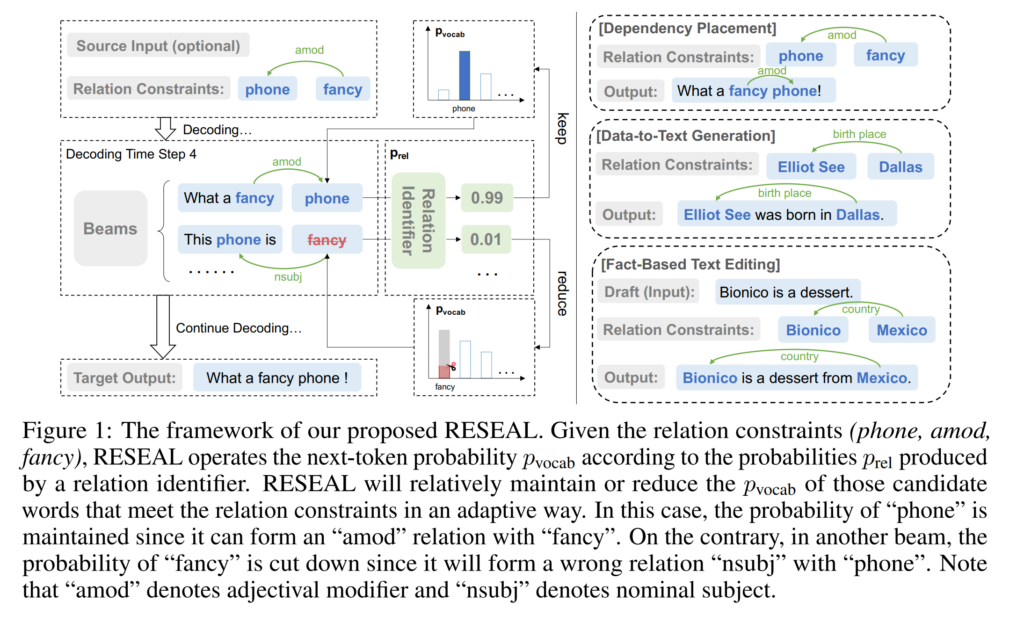
41. Relation-Constrained Decoding for Text Generation

Xiang Chen, Zhixian Yang, Xiaojun Wan. Peking University. NeurIPS 2022.
https://openreview.net/forum?id=dIUQ5haSOI

The paper describes a model for text generation, based on target dependency relations that should be in the output.
The word-level output probabilties are modified to increase the likelihood of generating words that match the target relation.
During beam decoding, the candidate construction method also takes the target relations into account.
Evaluation is performed on several datasets, formulating the task as text generation based on dependency relations.

42. Interpretability for Language Learners Using Example-Based Grammatical Error Correction

Masahiro Kaneko, Sho Takase, Ayana Niwa, Naoaki Okazaki. Tokyo Institute of Technology. ACL 2022.
https://aclanthology.org/2022.acl-long.496

Describes a system for performing error correction, while also returning examples of similar corrections from the training set. Each token in each sentence is encoded with the GEC model and the representation is used for finding other similar correction examples. The kNN-based similarity is also incorporated into the output distribution of the error correction model, improving performance on closed-class errors while reducing some performance on open-class errors.

43. Ensembling and Knowledge Distilling of Large Sequence Taggers for Grammatical Error Correction

Maksym Tarnavskyi, Artem Chernodub, Kostiantyn Omelianchuk. Ukrainian Catholic University, Grammarly. ACL 2022.
https://aclanthology.org/2022.acl-long.266

The paper extends the GECToR sequence tagging architecture for grammatical error correction.
The models are scaled up to bigger versions, multiple versions are ensembled together and then distilled back to a single model through generated training data. Improvements are shown on the BEA-2019 dataset both for the ensembled configuration and the single best model.

44. Linguistic Parameters of Spontaneous Speech for Identifying Mild Cognitive Impairment and Alzheimer Disease

Veronika Vincze, Martina Katalin Szabó, Ildikó Hoffmann, László Tóth, Magdolna Pákáski, János Kálmán, Gábor Gosztolya. University of Szeged. Computational Linguistics 2022.
https://aclanthology.org/2022.cl-1.5

Developing a system for the detection of cognitive impairment based on linguistic features.
Patients were recorded when answering free-text questions, their answers transcribed, and a large number of features extracted for classification.
Morphological and statistical features perform well across different tasks and the overall classifier achieves 2-class F1 of 84-86%.

45. Black-box Prompt Learning for Pre-trained Language Models

Shizhe Diao, Zhichao Huang, Ruijia Xu, Xuechun Li, Yong Lin, Xiao Zhou, Tong Zhang. The Hong Kong University of Science and Technology, University of California San Diego. TMLR 2023.
https://arxiv.org/abs/2201.08531

The paper proposes the task of tuning prompts for pre-trained models in a setting where the model weights or activations are not available and need to be treated as a black box.
A first stage of white-box fine-tuning using a small dataset is assumed, followed by a black-box tuning stage using additional data just for updating the prompts.
The prompts are updated by randomly sampling permutations to the existing prompts, then approximating the gradient using the natural evolution strategy (NAS) algorithm.
Evaluation shows that having the extra black-box training step on additional data is beneficial over only doing white-box prompt tuning using a smaller dataset, but is outperformed by using the full dataset for white-box prompt tuning.

46. Mind the gap: Challenges of deep learning approaches to Theory of Mind

Jaan Aru, Aqeel Labash, Oriol Corcoll, Raul Vicente. University of Tartu. ArXiv 2022.
https://arxiv.org/abs/2203.16540

An opinion paper on deep learning models in connection to the Theory of Mind – the skill of humans to understand the minds of others, imagine that they might have hidden knowledge or emotions. Gives a summary of different stages of this skill developing in humans, along with a review of this work in the deep learning field. Proposes that this is not a skill that will develop from one task, and that it should be evaluated through the interpretation of neural networks (for example whether a specific neuron can be identified to detect the emotion of others).

47. Atomic Inference for NLI with Generated Facts as Atoms

Joe Stacey, Pasquale Minervini, Haim Dubossarsky, Oana-Maria Camburu, Marek Rei. Imperial, Edinburgh, QMUL, UCL. EMNLP 2024.
https://arxiv.org/abs/2305.13214

Long texts are broken down into individual self-contained facts using an LLM. A special architecture then learns to make decisions about the text by making individual entailment decisions about those facts. The resulting system is able to point to specific facts as explanations for the overall decision, as these are guaranteed to be a faithful explanation for the final prediction.

48. Continuous Predictive Modeling of Clinical Notes and ICD Codes in Patient Health Records

Mireia Hernandez Caralt, Clarence Boon Liang Ng, Marek Rei. Imperial. BioNLP 2024.
https://arxiv.org/pdf/2405.11622

Investigates the task of early prediction of hospital diagnoses and necessary procedures, based on textual notes in the electronic health records. A causal hierarchical model is created, which is able to make predictions about overall ICD codes at every timestep of the hospital stay. As the note sequences are very long, an extended context algorithm is proposed, which samples a subset of notes during training but is able to iteratively use the whole sequence during testing.

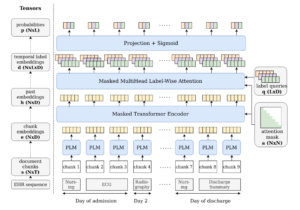
49. Modelling Temporal Document Sequences for Clinical ICD Coding

Clarence Boon Liang Ng, Diogo Santos, Marek Rei. Imperial, Transformative AI. EACL 2023.
https://aclanthology.org/2023.eacl-main.120.pdf

Assigning ICD codes to discharge summaries in electronic health records, which indicate the diagnoses and procedures for each patient. The model is designed to integrate additional information from the previous notes in the health record. Additive embeddings are used for representing metadata about each note. The system achieves state-of-the-art results on the task of ICD coding.

50. When and Why Does Bias Mitigation Work ?

Abhilasha Ravichander, Joe Stacey, Marek Rei. Ai2, Imperial. EMNLP 2023.
https://aclanthology.org/2023.findings-emnlp.619

Targeted testing of different model debiasing methods, in order to investigate their effect on the model. Creating six datasets that contain very specific controlled biases for probing debiasing methods. Experiments show that specifically debiasing against one bias actually increases reliance against another bias.

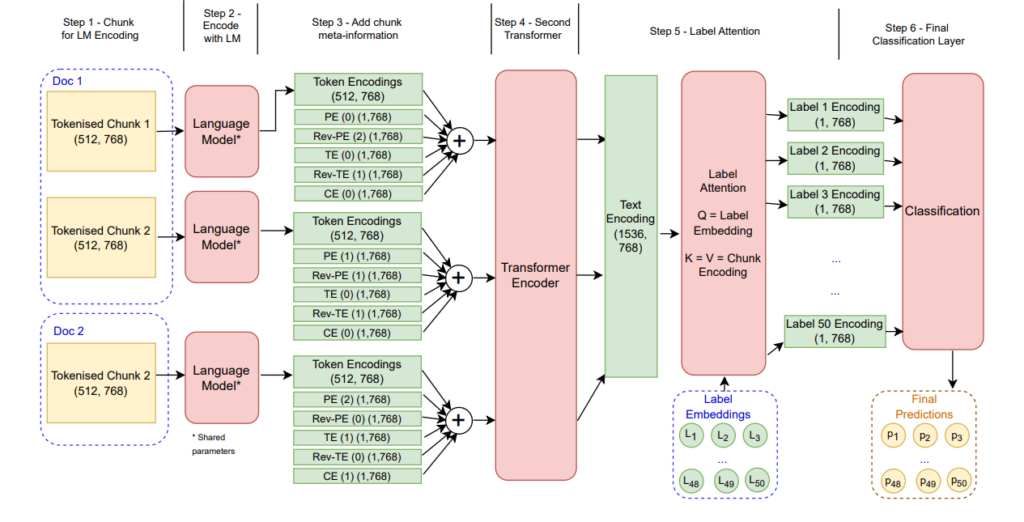
51. Did the Neurons Read your Book? Document-level Membership Inference for Large Language Models

Matthieu Meeus, Shubham Jain, Marek Rei, Yves-Alexandre de Montjoye. Imperial College London, Sense Street. USENIX Security Symposium 2024.
https://arxiv.org/abs/2310.15007

Introducing the task of document-level membership inference for LLMs – determining whether a particular document (e.g. book or article) has been using during the LLM training, while only having query access to the resulting model. All token-level probabilities are collected from the language model, these are normalised by how rare each token is overall, and then aggregated into features and given to a supervised classifier. Experiments show that most documents can be detected, with the detection working better for longer documents.

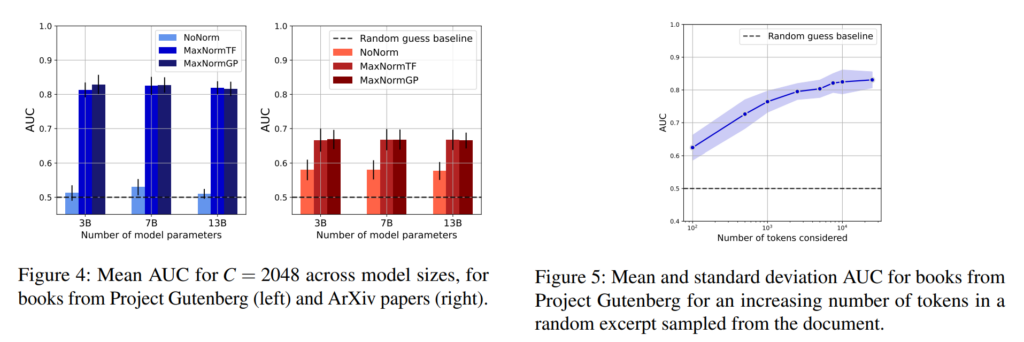
52. An Extended Sequence Tagging Vocabulary for Grammatical Error Correction

Stuart Mesham, Christopher Bryant, Marek Rei, Zheng Yuan. University of Cambridge, Imperial College London, King’s College London. EACL 2023.
https://aclanthology.org/2023.findings-eacl.119

Introducing tool usage into a tagging-based grammatical error correction model. Instead of training the model to correct every type of error itself, the model detects when a word should be sent to a separate spellcheck or an inflection system. The modification improves performance on the targeted error types and overall, also leaving room for introducing additional tools for other error types.

53. On the application of Large Language Models for language teaching and assessment technology

Andrew Caines, Luca Benedetto, Shiva Taslimipoor, Christopher Davis, Yuan Gao, Oeistein Andersen, Zheng Yuan, Mark Elliott, Russell Moore, Christopher Bryant, Marek Rei, Helen Yannakoudakis, Andrew Mullooly, Diane Nicholls, Paula Buttery. Cambridge, KCL, CUPA, Writer Inc, Imperial, ELiT. AIED LLM 2023.
https://arxiv.org/abs/2307.08393

Discussing the possible applications of generative language models in the area of language teaching. Covering tasks such as automated test creation, question difficulty estimation, automated essay scoring and feedback generation. The paper concludes that there is a lot of potential but for best results the automated systems need to be paired with human intervention.

54. Prompting open-source and commercial language models for grammatical error correction of English learner text

Christopher Davis, Andrew Caines, Øistein Andersen, Shiva Taslimipoor, Helen Yannakoudakis, Zheng Yuan, Christopher Bryant, Marek Rei, Paula Buttery. Cambridge, Writer Inc, KCL, Imperial. ACL 2024.
https://arxiv.org/pdf/2401.07702

Investigating the abilities of LLMs to perform grammatical error correction. 7 open-source and 3 commercial models are evaluated with 11 different prompts on established error correction benchmarks. LLMs perform the best on fluency edits but do not come close to state-of-the-art performance on minimal corrections of grammatical errors.

55. Control Prefixes for Parameter-Efficient Text Generation

Jordan Clive, Kris Cao, Marek Rei. Imperial, DeepMind, Cambridge. GEM 2022.
https://aclanthology.org/2022.gem-1.31

Introducing control prefixes, which are plug-and-play modules for influencing text generation into a particular direction. By switching on a particular control prefix, the model can generate text in a particular domain, in a particular style or at a specific length. Experiments also include predicting values for a previously unseen generation category.

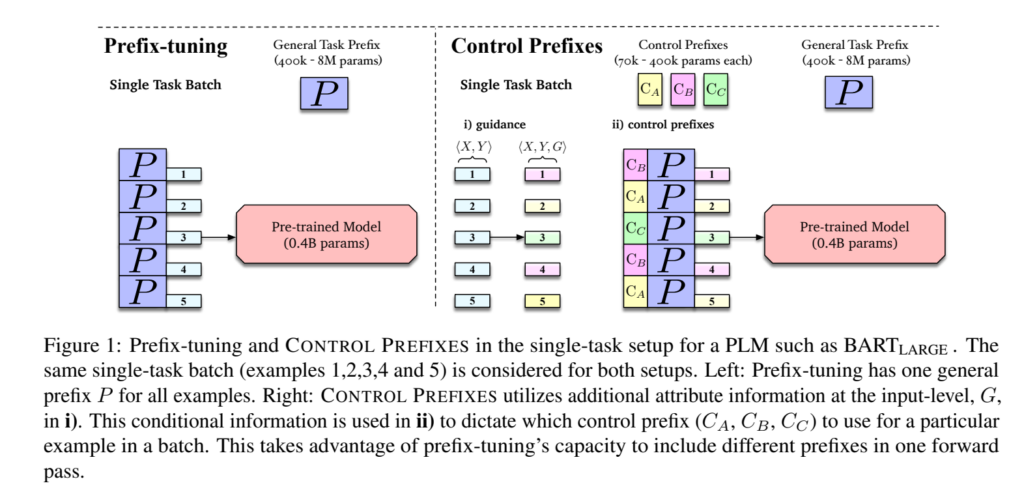
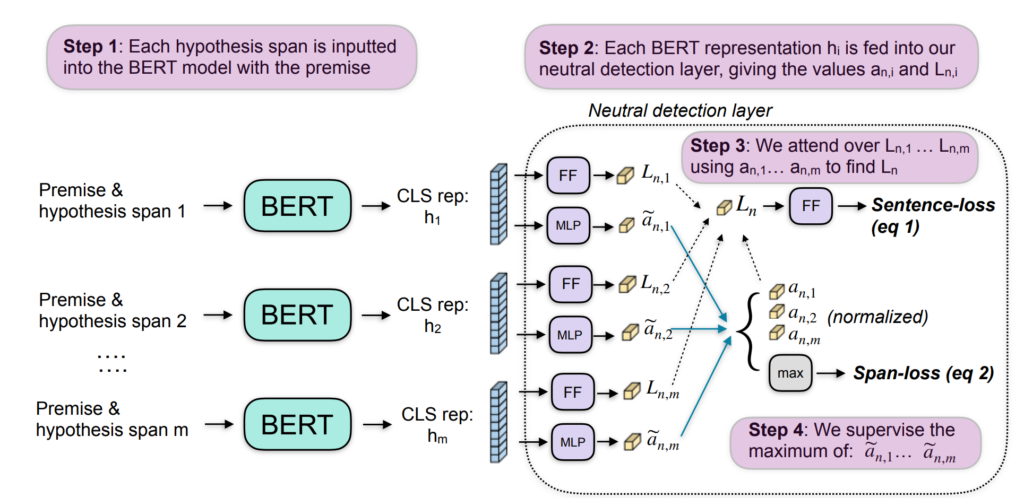
56. Logical Reasoning with Span-Level Predictions for Interpretable and Robust NLI Models

Joe Stacey, Pasquale Minervini, Haim Dubossarsky, Marek Rei. Imperial College London, University of Edinburgh, UCL, Queen Mary University of London. EMNLP 2022.
https://aclanthology.org/2022.emnlp-main.251

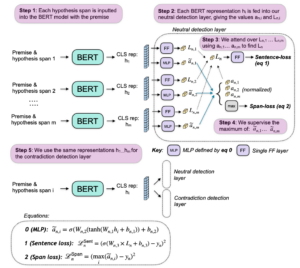
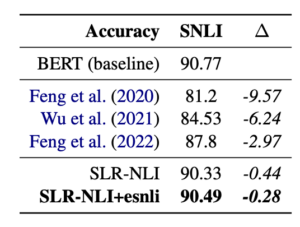
A neural architecture for entailment detection (NLI) that has guarantees on the faithfulness of its explanations. Text is broken into shorter spans, the model makes predictions about each span separately and the final overall decision is found deterministically based on the span-level predictions. The updated model retains performance while being more explainable, and also outperforms all previous logical architectures for entailment detection.

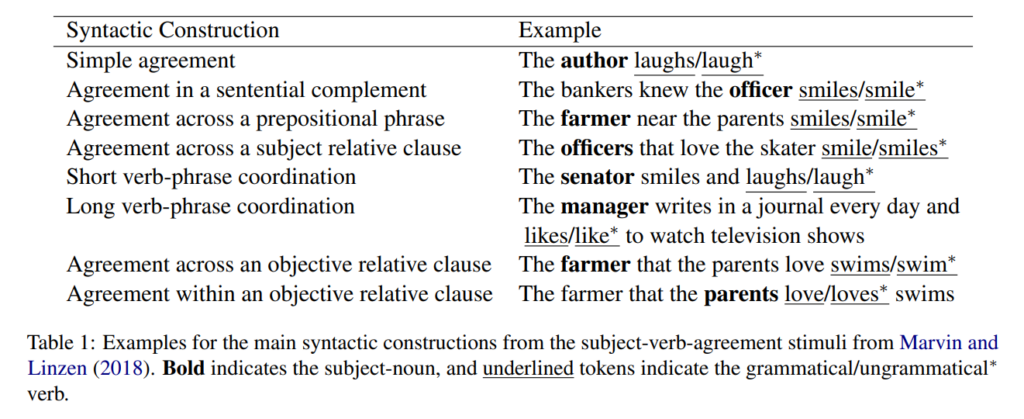
57. Probing for targeted syntactic knowledge through grammatical error detection

Christopher Davis, Christopher Bryant, Andrew Caines, Marek Rei, Paula Buttery. Cambridge, Imperial. CoNLL 2022.
https://aclanthology.org/2022.conll-1.25

Investigating how much pre-trained language models capture syntactic information and how well are they able to detect syntactic errors out-of-the-box. Different language models are frozen and small probes are trained on top of them to identify specific errors in text. Analysis shows that the final layers of ELECTRA and BERT capture subject-verb agreement errors best.

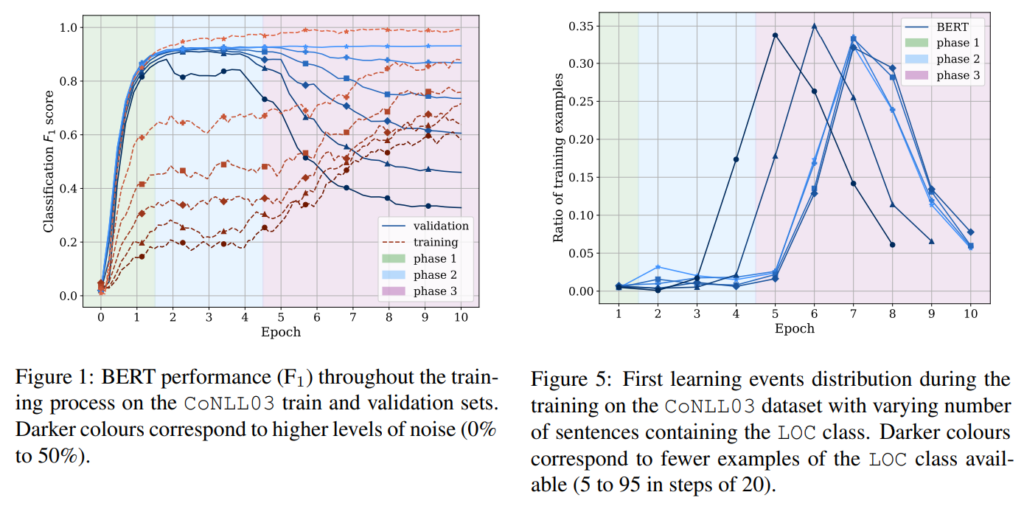
58. Memorisation versus Generalisation in Pre-trained Language Models

Michael Tänzer, Sebastian Ruder, Marek Rei. Imperial, Google Research. ACL 2022.
https://aclanthology.org/2022.acl-long.521

Investigating the learning abilities of language models under controlled experiments. Results show that LMs are surprisingly resilient to noise in the training data, with the resulting performance being nearly unaffected as long as the learning is stopped at an optimal time. However, the models are not able to differentiate between label noise and low-resource classes, with overall performance deteriorating just as the rare classes start to be learned. The paper proposes a model based on class prototypes to get the best of both worlds.

59. Multimodal Conversation Modelling for Topic Derailment Detection

Zhenhao Li, Marek Rei, Lucia Specia. Imperial. EMNLP 2022.
https://aclanthology.org/2022.findings-emnlp.376

Creating and releasing a dataset of reddit threads that contain images. Posts that derail the conversation are then identified and annotated with the derailment type, such as starting a new topic, spamming or making toxic comments. A multimodal architecture for this task is also described, which encodes the post, the image and the context in order to make accurate decisions.

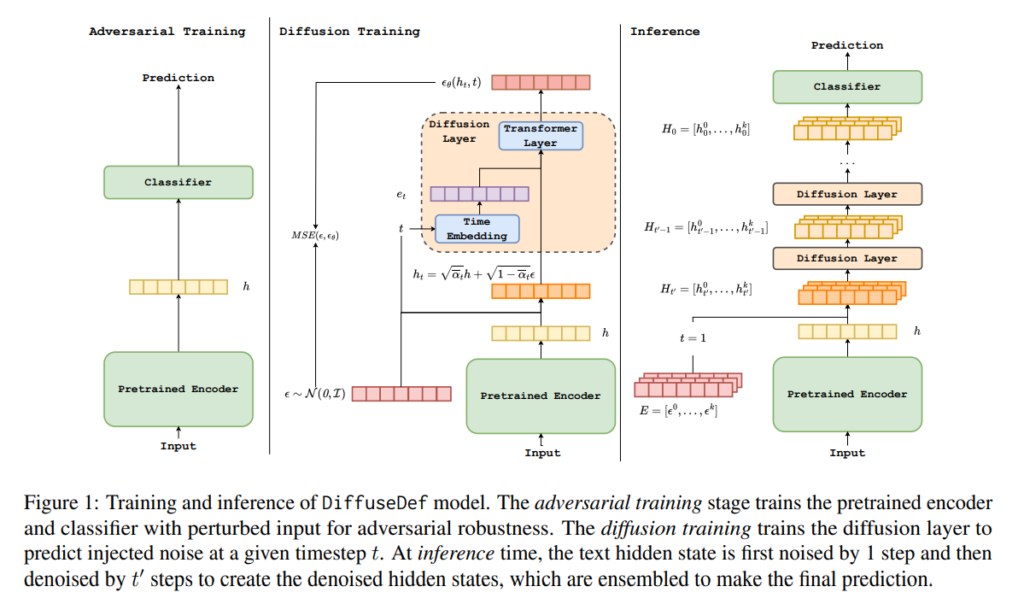
60. DiffuseDef: Improved Robustness to Adversarial Attacks

Zhenhao Li, Marek Rei, Lucia Specia. Imperial. ArXiv.
https://arxiv.org/abs/2407.00248

Introducing a defusion module as a denoising step for text representations in order to prevent adversarial attacks.
The diffusion layer is trained on top of a frozen encoder to predict the randomly inserted noise in the representation.
During inference, this noise is then subtracted over multiple iterations to get a clean representation.
Results show state-of-the-art results for resisting adversarial attacks.

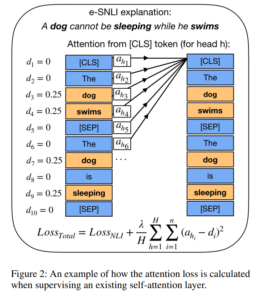
61. Supervising Model Attention with Human Explanations for Robust Natural Language Inference

Joe Stacey, Yonatan Belinkov, Marek Rei. Imperial, Technion. AAAI 2022.
https://cdn.aaai.org/ojs/21386/21386-13-25399-1-2-20220628.pdf

Investigating how natural language explanations of particular label assignments can be used to improve model performance.
The method identifies important words in the input, either based on explanation text or highlights, and then trains the model to assign higher self-attention weights to those tokens. Experiments show that this method consistently improves performance, making the model focus more on the relevant evidence.

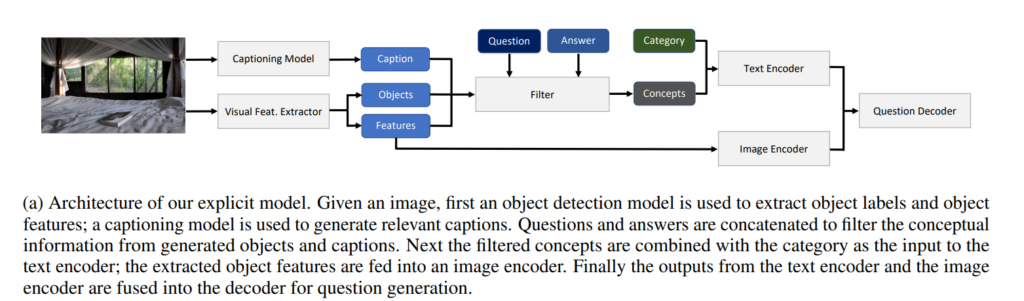
62. Guiding Visual Question Generation

Nihir Vedd, Zixu Wang, Marek Rei, Yishu Miao, Lucia Specia. Imperial. NAACL 2022.
https://aclanthology.org/2022.naacl-main.118.pdf

Investigates guiding the process of visual question generation, where the system generates questions about a given image.
The architecture allows the user to specify categories or objects in the image, which the system will then ask about.
These choices can also be modeled as latent variables inside the model, leading to state-of-the-art results in regular VQG.

63. Finding the Needle in a Haystack: Unsupervised Rationale Extraction from Long Text Classifiers

Kamil Bujel, Andrew Caines, Helen Yannakoudakis, Marek Rei. Imperial, Cambridge, KCL. Arxiv 2023.
https://arxiv.org/pdf/2303.07991

Designing a hierarchical transformer model that is able to explain itself by pointing to relevant tokens in the input.
It indirectly supervises the attention on a certain number of tokens at each turn, in order to make the model behave like a binary importance classifier on the token level. Previous methods that work well on shorter texts (e.g. individual sentences) are shown to not work well when applied to longer texts.

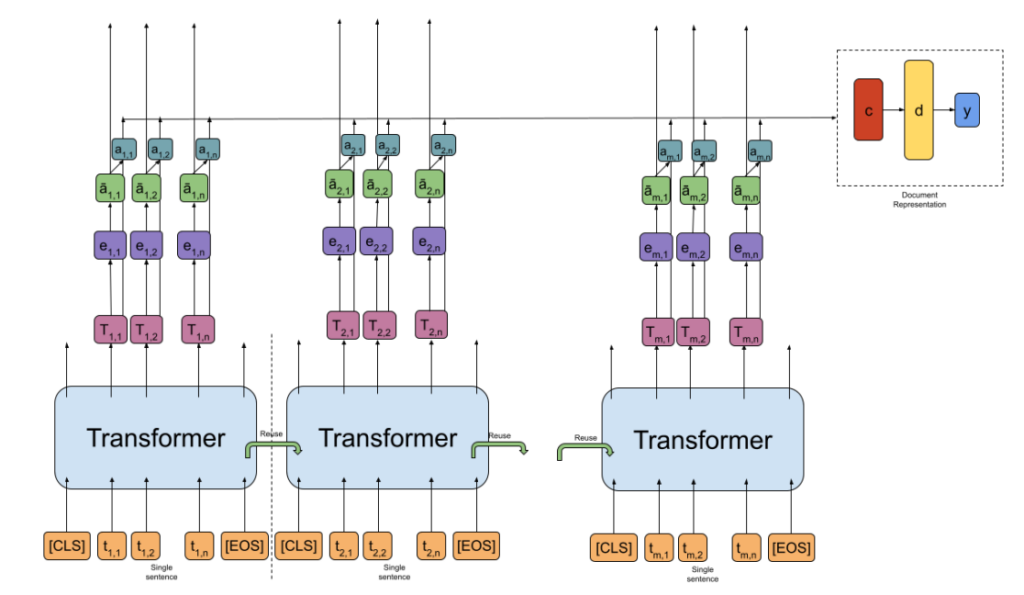
64. Distilling Robustness into Natural Language Inference Models with Domain-Targeted Augmentation

Joe Stacey, Marek Rei. Imperial. ACL 2024.
https://aclanthology.org/2024.findings-acl.132.pdf

Investigating model distillation methods that would be better able to generalise to previously unseen domains. The methods either generate new unlabeled examples or upweight existing examples from the training data that are more similar to a particular domain, then use these as input during the distilling process. Experiments show that this increases robustness also towards domains which are not considered during distillation.

65. The alignment of companies’ sustainability behavior and emissions with global climate targets

Simone Cenci, Matteo Burato, Marek Rei, Maurizio Zollo. Imperial. Nature Communications 2024.

Applying NLP systems to analyse thousands of company reports and the sustainability initiatives described in those reports.
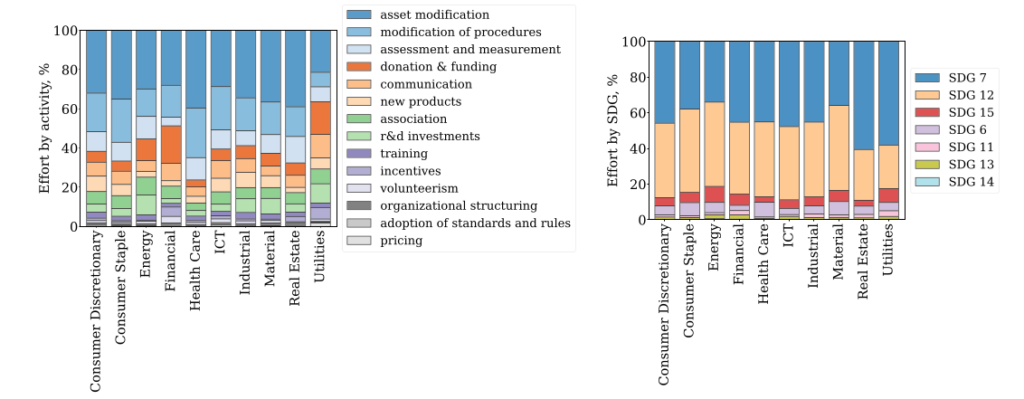
The system crawls public reports online, extracts sentences that refer to sustainability initiatives implemented by that company, and classifies them based on type, stakeholder and one of the 17 Sustainable Development Goals established by the UN.
Analysis indicates that companies are mostly investing in risk-prevention initiatives, as opposed to innovation and cooperation.

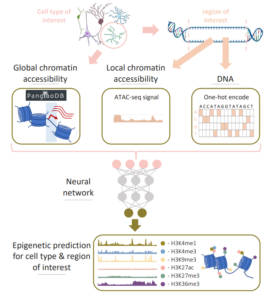
66. Predicting cell type-specific epigenomic profiles accounting for distal genetic effects

Alan E Murphy, William Beardall, Marek Rei, Mike Phuycharoen, Nathan G Skene. Imperial, Manchester. Nature Communications 2024.
https://www.biorxiv.org/content/10.1101/2024.02.15.580484

Using architectures based on pre-trained transformer language models and extending them for the domain of genome modeling.
Proposing and releasing Enformer Celltyping, which can incorporate long-range context of DNA base pairs and predict epigenetic signals while being cell type-agnostic.

67. SoK: Membership Inference Attacks on LLMs are Rushing Nowhere (and How to Fix It)

Matthieu Meeus, Igor Shilov, Shubham Jain, Manuel Faysse, Marek Rei, Yves-Alexandre de Montjoye. Imperial, Sense Street, Université Paris-Saclay. Arxiv 2024.
https://arxiv.org/pdf/2406.17975

In order to develop methods for detecting whether specific copyrighted work has been used for training a particular LLM, researchers have collected datasets of known documents that are (or are not) part of specific training sets. However, these datasets are normally collected post-hoc, leading to distibution differences. The experiments show that many detection models misleadingly react to those differences, instead of truly detecting the documents in the training data. Suggestions are provided for preventing this issue in future experiments.

68. StateAct: State Tracking and Reasoning for Acting and Planning with Large Language Models

Nikolai Rozanov, Marek Rei. Imperial. Arxiv 2024.
https://arxiv.org/abs/2410.02810

Improving LLMs for long-range planning and reasoning, for tasks which require a large number of steps to complete.
As the length of the few-shot examples and the generated trace grows longer, LLMs can lose track of what they are supposed to do and what they have done already. Periodically reminding them of the task and explicitly keeping track of their state provides consistent improvements in performance, establishing a new state-of-the-art result for the Alfworld benchmark.

If you would like to receive email updates about the latest articles, leave your details below.

Name:

Email address:

Leave this field empty if you're human:

This is a collection of advice that I give to students doing research projects in NLP/ML/AI. It includes suggestions that I wish I had known when I myself first started, as well as lessons from supervising students in previous years.

I would recommend reading this once before starting your project, then again after about a month or two into the project. Different things will seem relevant to you.

Implementation and debugging

1. Don’t assume that your code is bug free – check and debug. Deep learning code can be difficult to get right. Make sure the tensors have the right shapes and dimensions. Occasionally you’ll need to think in 5 dimensions and it’s easy to get it wrong. Make sure you know what the library functions are actually doing instead of blindly applying them. Some pytorch and tensorflow functions make it easy to apply complicated operations but they also make it easy to confuse what their input and output actually contain. It is always a good idea to test sections of the code with small toy examples.
2. Whenever you assume something about your data or output, put an assert into the code which will check that this assumption is always true. For example, if you know how long the input list should be or that the output should contain only values in a certain range. Many times this has helped me catch issues that I didn’t expect.
3. While automated checks are useful, they won’t catch everything. So you also have to manually check your model output and performance. Make sure that the output looks as expected and that the results make sense. If you expect one configuration to perform better than another, but the results show something different, then investigate and figure out why that is. Sometimes you find a bug, other times you learn something new about the model or the task.
4. When your model isn’t learning anything, there are two diagnostic tests I recommend running: 1) Make sure that your model can memorize a small training set. For example, a model should be able to easily memorize (get 100% performance) a training set with 10 examples. If not, this indicates a problem with the code or the data. 2) If your model takes features, give the label as an input feature and train on the whole dataset. Evaluate on the dev set, also giving labels as input features. The model should get perfect performance both on the train and dev set. If not, this indicates issues with network connections or optimization.
5. During training, evaluate performance on the training and development sets at certain intervals. For most models, the performance on both will initially go up. Then at some point performance on the development set will start to drop while the performance on the training set will keep improving, which indicates overfitting. To deal with this, use early stopping – store a copy of the model whenever it outperforms all previous iterations on the development set. Once the training is done, load back the stored best model. To avoid unnecessary training time, you can stop the training when the best performance on the development set hasn’t improved for a certain number of epochs. This is a robust default strategy for training neural models. If you use some other strategy, then best to cite the paper where you got it from. Note: Early stopping is becoming less important with large pre-trained language models and it’s common to just train for a fixed number of 2-3 epochs. We have some experiments investigating this here.
6. Use version control and external backups. You don’t want to suddenly lose all your hard work. It’s also frustrating when you get your system to work, make some edits that break it and then have no idea which exact edits need to be reversed. Git is good, Github and Bitbucket both allow free private repositories.
7. Hyperparameter tuning is still a dark art, as specific values often interact with other parameters and it’s not computationally feasible to actually try all of their combinations. With time and experience, you will get better at predicting which parameters work best for specific architectures. Until then, start with parameter values that others have used in related work and explore how changing different values, in isolation or in small parameter groups, affects the model.

Evaluation

8. Put extra care into making sure that the evaluation is implemented correctly. If you have bugs in your model, then the model usually won’t work well and you would discard it. But if you have bugs in your evaluation, you might end up reporting high results for a model that doesn’t actually work. Finding out later that your published results are all imaginary is not a situation you want to be in.
9. Make sure to set up separate train/dev/test sets. Use the training set for parameter optimization, the development set for choosing hyperparameters and early stopping, and the test set for final evaluation. You can use the training set in more flexible ways, but you’re not allowed to edit or subsample the test set. For example, you can leave out sentences that are too long in the training set, but you can’t do that for the test set. It needs to remain fixed in order to be comparable to other published results. Cross-validation is also an option if the dataset is too small for a fixed split. If previous researchers have split the data already, then you need to use the same splits as them; don’t create a new split without a strong reason.
10. Learn to handle randomness in your models. Random seeds affect various parts of the processing stream – shuffling of the data, initialisation of the weights, etc, so it’s a good idea to try to set them. However, sometimes neural components will give random results anyway. This is down to how the toolkits are implemented and we don’t have much control over them. GPU operations are highly parallel and when results finish at different times, some functions can combine in different order, which results in small rounding errors. These can compound and cause noticeably different results when running the same experiment multiple times, even when controlling the random seeds. To compensate for this, I usually run each experiment several (e.g. 10) times and report the average result. For full scientific rigor, you should also calculate and report the standard deviation and/or confidence interval of these results. Unfortunately, many people just tend to report a single result from a neural model, which in some cases can be a misleadingly high value that is later difficult to replicate.
11. Compare performance to published results to understand if your model is working as well as it should. Find a similar model in literature, set up your model configuration based on theirs, train on the same data and see if you are able to replicate their results. If you are working on an established task, start by getting your baseline performance to the previous state-of-the-art level. That way any improvement that you achieve will set a new state-of-the-art. It is tempting to show improvements over a weaker baseline, but pretty much anything will give an improvement if the baseline is weak enough. Trying to explain why your best system is still outperformed by a stronger baseline would be a massive headache later when trying to publish or defend your work.
12. Perform significance tests on your final results when possible. It adds credibility to your results. I recommend the randomization test, but any test is better than no test. If you show a significant improvement through an actual significance test, make that clear in the paper and state the test that was used. However, if you haven’t performed any significance test, then do not use phrases like “results are significantly better” when describing your work as that will appear misleading.
13. If your novel system has multiple novel components, then for a convincing evaluation you need to perform an ablation experiment. This means either a) removing individual components from the full system to see how much performance drops, or b) incrementally adding individual components to the simple system to see how much performance improves at each step. The goal is to measure the benefit of each component separately, to make sure that they all are actually useful. Otherwise, if you only evaluate the combined system, then it could easily be that only one modification is providing all the improvements and the others are useless or even lowering performance.

Project planning

14. In the beginning of your project, start by reading the papers related to your topic. If you only know a small number of related papers, try looking at the papers that are referenced in these. Google Scholar also has a “Cited by” button at each paper that will show you other later papers that reference this particular paper. Simple keyword searches on Google and ArXiv are useful too. Get familiar with the current state-of-the-art, try to get ideas that you can integrate into your project, while also looking for existing models that you can compare against. If you don’t yet feel comfortable with the toolkits that you will be working with, focus on getting some practice with these as well.
15. If there is any previous work on your task, ideally the state-of-the-art, then start by reimplementing that. If they already have the code available then great, just get it running. Otherwise, write the code, train the model on the same data and evaluate the same way as they do. If you get the same results, then great, you know that your system and evaluation are working. If not, debug and improve until they are working, or find out exactly what is the cause of the difference. You don’t want to have a fundamental bug somewhere deep in your code all throughout the project.
16. Implement a simple version of your idea early and quickly. Don’t spend a long time designing and implementing a complex architecture in the beginning. Instead, start by implementing and training the simplest system you can imagine, which shouldn’t take longer than a week or two. Make sure you are getting reasonable results and that the evaluation is set up properly. Only then you should build on it and improve the results with more complex models. It is much easier to debug a basic system and this will give you a chance to get to know the problem and the dataset. Plus, you can always use the original model as a baseline in your work.
17. Make a plan, even if you don’t follow it. Making a plan is a useful exercise, as it makes you think through all the different parts of the project that need to be completed, how they fit together, how much time they might take and what might go wrong. After you have created the plan, you will have a reasonable idea in which direction you are going, hopefully sanity-checked by your supervisor. However, once you actually start work on the project, you will learn new things about the problem and get better ideas, so this plan is likely to change and improve. And that is fine. The main thing is to always have a plan for where you are heading based on current information; when you get new information, feel free to revise that plan.
18. Whenever possible, aim to push the state-of-the-art performance on your task. There are exceptions and chasing the highest number should not be a goal by itself, but it helps with making sure that your contribution is actually advancing the field. Otherwise, showing improvements only over a trivial baseline will imply that this problem has already been solved by other methods but you are trying to ignore or hide them. On the other hand, if you start with an existing state-of-the-art system and improve on that, then it is much easier to claim that you have made a novel and useful finding. Setting a new state-of-the-art also usually means it will be easier to publish this work as a paper.
19. When brainstorming ideas, think in terms of what additional information or capability is not currently available to the model but would help it make better decisions. Trying to blindly integrate the flavor-of-the-month ideas into every model is not a good strategy.
20. When using computation resources that have quotas, make sure to use your available time/credit sensibly. Estimate how long your experiment will take (or set a limit), multiply by the number of jobs you are starting and make sure the speed at which you are spending credits lasts you until the end of the project. If you’re just starting, better start cautiously, your code is likely to still have bugs and you might need to rerun all of these experiments anyway. If you’re finishing the project and know exactly which experiments are left to write a good report, you can take full advantage of the parallel computation. Just be sensible – every year there is someone who blows their whole GPU cluster credit in the first week of the project. You don’t want to be stuck training your neural models on CPUs.
21. Look at some existing dissertations to get a feel for what they should look like and what kind of content is expected. Do that in the beginning of the project, as opposed to the end.
22. When choosing topics to work on, I recommend choosing something that is close to your heart and something that makes a difference and drives the field forward. In the past, I have found myself solving a question only to realise that it doesn’t really need to be answered.
23. Reading related work is very important, but try to learn from other fields as well. Read about research in different areas of machine learning, NLP, cognitive science, neuroscience, linguistics, vision and signal analysis. By broadening your world view, you can bring new ideas to your research topic and find new exciting applications in other domains.
24. If your group has reading groups, take active part in them. They motivate you to read papers outside of your narrow topic, which expands your view and can give new ideas that can be adapted for your project. Reading groups also encourage interaction between the group members and this can lead to very interesting discussions. Volunteering to present allows you to choose the topic that you would like the group to discuss, lets others know what you are working on and it’s a good way to get some experience with public speaking. 

Writing and Publishing

25. Start writing early. Don’t underestimate the difficulty of writing up a project report. Communicating your research, motivation and architectures clearly to the reader and presenting a coherent story takes effort. Plus, you might find during writing that in order to present a full picture you need to go back and run some additional experiments. Finish your write-up early enough so that someone, probably your supervisor, has time to read it though and give you feedback and you have time to implement changes based on this feedback.
26. Proof-read your writing. This applies to any writing – reports, dissertations and papers. Grammatical errors, spelling errors and repeated words leave an overall sloppy impression and can bias a reviewer in a negative direction even if the work itself is good.
27. I usually recommend aiming to publish a paper based on your project. Publishing your findings is important for the field and having a peer-reviewed publication makes your CV positively stand out in future applications to any research-related positions. It is the same work you will be doing for your report/dissertation anyway, might as well also get a paper out of it. You just have to make sure that the work is good enough to be publishable.
28. Many venues provide an opportunity for a rebuttal, to reply to the reviewers. These don’t result in an increased score very often, but it is still useful to write one – as an exercise for yourself and to better inform the reviewers, so that they get an informed picture of your paper. Focus on the areas that can be objectively argued, for example, if they have misunderstood something. Sometimes the reviewer just subjectively doesn’t like the paper and there’s not much that can be done about that.
29. Papers get rejected, it’s very common and happens to everyone. Use this as a learning experience, improve the paper based on the feedback and then resubmit. Improvements can include additional experiments that the reviewers requested, clarifying areas that confused them or changing the way that the work is presented in order to focus more on a slightly different aspect.
30. Most of the time you will not agree with the reviewers’ comments. You will probably think “Are they stupid? I clearly covered that issue in Section X”. You’ll have to accept the fact that reviewer quality varies quite a lot and most of them have very little time to devote to your paper. That is why it’s up to you to make the paper so clear and well-written that even the worst reviewers are able to follow it. Standing your ground and fighting with the reviewers will not get your paper accepted. Instead, think about how you can convince the reviewers or best clarify their misunderstandings. The reviewers represent a sample of your potential future readers as well, so any improvements you make also translate to your audience understanding the paper better.
31. In terms of the author list, the main author usually goes in the first position, the main supervisor in the last position and everyone else who substantially contributed to the paper would be added in between.
32. Read the submission requirements provided by the conference/journal and stick to them. These are quite strict. Being over the page limit by one line is enough to get the paper rejected even without a review. Messing with the page margins and font sizes will also disqualify a paper. Make sure to use the required latex template for that particular conference – they will vary between conferences.
33. ArXiv is a useful place to submit a paper for extra publicity. It acts as a version-controlled repository of non-peer-reviewed research papers. Some things to keep in mind: 1) Anyone can upload any paper to ArXiv so having it there is not the same as publishing it at a conference or journal. 2) Once you upload a paper, it is there forever. You can still update the paper but the old versions will also be publicly visible. 3) Many conferences now have a mandatory anonymity period, which extends before the submission deadline, during which you can’t upload the paper anywhere, including arxiv. That means you either need to complete and upload the paper before this period starts or you have to wait until the conference decisions have been sent out. 4) ArXiv keeps the source latex of your paper and it will be available for anyone to download. You might want to clean it up a bit before submitting, removing notes and comments that are not meant for the public.
34. Don’t be afraid to reach out to researchers beyond your immediate research group. This can be in order to ask for clarification about a paper they have published or initiating a collaboration. They can bring in new expertise and ideas, which would benefit everybody.
35. When collaboratively writing a paper, Overleaf is a good platform to use. Many universities have a paid subscription to Overleaf – try adding your university email to your account to see if you get upgraded for free. It should work for Imperial and Cambridge.
36. Do not use Apple’s Preview or Quartz for creating your pdfs. It has been known to create pdfs that cannot be opened by Adobe Acrobat. This in turn can lead to a paper being rejected without review. Use pdflatex or download the pdf from Overleaf.
37. If you need to submit an Early Stage Report (this is specific to Imperial) or a background report, create this as a very early version of your thesis/dissertation. Structure the report similar to how you would structure the thesis. Have a clear background section that covers previous work. And use the style files that you would for a thesis. You can then extend this same report for your final work later.

Interacting with your supervisor

38. Remember that you are in charge of your project. The role of the supervisor is to give advice and to help direct you onto a promising path. But this is your research project, so the supervisor is not supposed to plan out every experiment that needs to be run. It is up to you to plan your research (with the help of your supervisor), decide which experiments need to be run and also brainstorm new ideas. Take active charge of your project and set your own targets, instead of expecting to tick off a weekly checklist created by the supervisor.
39. At the same time, listen to your supervisor. If they tell you to do something specific, you should probably do it. This can be your first similar project whereas they have done many of them before. They most likely know more about the field and what is necessary in a report or paper. Ideally, they will give you freedom to explore, but if they tell you to get something specific done then there is probably a good reason for it.
40. Meet your supervisor, ideally once a week. Use this to give an update on your work and discuss any questions you might have. The regular weekly meeting helps to keep you motivated and progressing each week.
41. Your supervisor is probably working with many more projects in addition to yours. When you meet up after a week, it’s good to give a bit of context and summary regarding the state of the project and which part you are currently focusing on, before jumping into the fine-grained details. This helps get the supervisor onto the right wavelength.
42. The supervisor is not always right. Listen to them and their arguments, as they probably have more experience than you. But if you are still not convinced then find a way to learn more or try your idea out empirically. In the worst case, you will learn something new. The supervisor wants what’s best for you, but they’re not all-knowing oracles. I’ve heard plenty of stories about supervisors in the early 2010’s telling their students not to work on neural networks because ‘that field isn’t going anywhere’.
43. Feel free to contact your supervisor with questions. Don’t wait until the next meeting if you have a question that stops you from progressing. However, please don’t send your supervisor questions that you can answer by googling.
44. During the project you should become more of an expert on your specific research topic than your supervisor. The supervisor provides a starting point, a broad overview and the experience. But it is your job to go in depth and find out everything you can about the specific questions that you are trying to answer in your project – get to know the previous related work, the latest developments, the available datasets and benchmarks, etc. For at least a short moment, you should be the world-leading expert on your very narrow research question.

If you made it this far, well done. If you are just starting with your project, I imagine some of these points might not mean much to you yet. I recommend going through this list again after you have worked on the project for a month or two.

It is about time we once again take a look at the publication statistics of the past year. 2019 was another record breaking year in machine learning and NLP research. Nearly all conferences had more attendees and more publications than ever before. For example, NeurIPS had 6,743 submissions and 1,428 accepted papers, which eclipses all the previous iterations. Because the conference sold out so fast last year, the organizers had to implement a randomised lottery for the tickets this time.

In this post you will find a number of graphs to illustrate the publication patterns from 2019.
I have included the following conferences and journals: ACL, EMNLP, NAACL, EACL, COLING, TACL, CL, CoNLL, NeurIPS, ICML, ICLR, AAAI. The paper information is crawled and processed automatically from the corresponding proceedings. While names and titles are quite easily accessible, getting the author affiliations is the noisiest part of the process, as this needs to be extracted directly from the pdf files. I've kept improving the pipeline every year so it should be more accurate than any of the previous iterations. If you do spot some mistakes, let me know.

The analysis this year includes some brand new statistics and graphs. This is thanks to Jonas Pfeiffer (@PfeiffJo) and Andrew Caines (@cainesap) who annotated the extracted organization names with origin countries. Andrew started the process with a subset of 2018 conferences for our joint article on The Geographic Diversity of NLP Conferences. Jonas then scaled this up to cover all of the organizations in all the conferences in this analysis. This allows us to create some new country-specific visualisations, which you'll see below.

While this post highlights authors and organizations who have published the most in the past year, I want to emphasize that publication quantity should not be used as the main metric for good research. It's always better to have one really groundbreaking and influential piece of work over 10 forgettable and incremental papers. These statistics are just meant to give an informative overview of the most active publication centres in this field and hopefully inspire some new researchers to publish their own ideas.

Venues

Essentially all conferences had record-breaking numbers of publications in 2019. The journals have a fairly stable publication rate, COLING and EACL didn't happen this year, and every other conference just grew substantially. NeurIPS is by far the biggest conference and it now has a lead of nearly 300 papers over AAAI.

Organizations

Let's see which organizations published the most in 2019. Google has taken a comfortable lead, publishing a substantial number of papers in every venue. They had more than twice as many papers at ICML as the next closest organization (MIT). Worth noting that in previous years I included DeepMind papers also under Google, whereas this time DeepMind is separated as its own entity. Microsoft and CMU are also publishing an impressive amount of research.

Next up, we can see the overall stats between 2012-2019. While Google is dominating the previous year, CMU and Microsoft are still ahead in the marathon. Notably, the counts for CMU and Microsoft came out identical(!), with 1,215 papers from both organizations. After them, the main heavy hitters are Google, Stanford, MIT, IBM, Berkeley and Tsinghua.

If we look at the separation in time, we see that Google is sort of a late bloomer. Compared to Microsoft and CMU they were publishing much less between 2012-2016, but have overtaken everyone else by quite a bit after that. All of the top players seem to have an upward trend and they all published more in 2019 than ever before.

Authors

Looking at individual authors, Sergey Levine (Berkeley) published an impressive 33 papers in 2019 - 12 in NeurIPS, 6 in ICML and 15 in ICLR. The other top authors are Graham Neubig (CMU), Yoshua Bengio (Montreal), Zhiyuan Liu (Tsinghua), Tao Qin (MSR) and Tie-Yan Liu (MSR).

Looking at the whole period of 2012-2019, we see that Yoshua Bengio (Montreal) has overtaken Chris Dyer (DeepMind) as the most prolific author. Ming Zhou (MSR), Yue Zhang (Westlake), Noah A. Smith (Washington) and Ting Liu (Harbin) all have more than 90 papers from that period. I have had to remove Yang Liu from the list, as there seem to be two or more people publishing under this name and I was not able to automatically separate them.

And looking at the separation in years shows that Sergey Levine, Graham Neubig and Yoshua Bengio have all overtaken the previous publication record set by Chris Dyer in 2016. They each also published considerably more than they did in the previous years.

First Authors

The authors with the highest publication counts are often the leaders of large groups, coordinating the work. But now let's see the first authors, who are usually the people doing the actual implementation and writing. Gabriele Farina is a 4th year PhD at CMU and he has authored 6 papers in 2019, half of them at NeurIPS. Ilias Diakonikolas (UW Madison), Hanrui Zhang (Duke), Rui Zhang (NUS), Chuhan Wu (Tsinghua), Pengcheng Yang (Peking), Sanjeev Arora (Princeton), Zeyuan Allen-Zhu (MSR) and Mikhail Yurochkin (IBM) were all first authors to 5 publications.

Looking at first-author papers through time, Zeyuan Allen-Zhu (MSR), Jiwei Li (Shannon AI), Ivan Vulić (Cambridge), Ryan Cotterell (Cambridge), Young-Bum Kim (Amazon) and Sanjeev Arora (Princeton) have published the most overall.

Countries

For the first time we are now actually able to analyse which countries published the most in 2019. Admittedly, this graph mainly highlights just how much the US dominates the research in this area. China, UK, Germany and Canada are also putting in a strong effort. China has a proportionally very large presence at AAAI, whereas the US is publishing more in NeurIPS and ICML.

The picture looks very similar when looking at the whole 2012-2019 period.

Through the years, the US has always published much more than everyone else and now the pace has accelerated even more. China is also trying to match this and has increased the lead over all the others by quite a bit. The UK is in a respectable third position.

USA

We can also take a look at the 2019 publishing statistics of individual organizations within each country/continent. Given how much the US publishes, the graph here looks sort of similar to the overall statistics, with Google in the lead.

China

In China, Tsinghua and Peking universities distinctly stand out in terms of publication numbers. The other top ranks are also mostly held by universities, with Baidu and Alibaba being the main industry publishers.

UK

In the UK, DeepMind takes the lead. They are followed by Cambridge, Oxford, Edinburgh, UCL, Imperial and the Alan Turing Institute. Worth noting that the Turing institute is largely virtual, so academic there often have affiliations with other universities as well. Out of the top 7, Cambridge and Edinburgh publish quite a bit in NLP, while the others are focusing mainly on ML.

Germany

In Germany, Darmstadt is the top publisher, with 2/3 of the papers in published in the area of NLP. Bosch is putting up some competition, ranking second with mostly ML papers. Saarland, LMU Munich, Tübingen, TU Munich and the Max Planck Institute for Intelligent Systems are also represented at the top.

Canada

Among the Canadian organizations, University of Toronto stands out with an impressive publication count. Université de Montréal and the Vector Institute are also at the top, along with Alberta, McGill, Waterloo, MILA and University of British Columbia. University of Waterloo seems to be the only one with a larger focus on NLP, with the others publishing mostly in the general ML conferences.

Topic Similarity

To try and capture a bit about the topics in the papers as well, I ran them through LDA and then visualised the results with t-SNE. Looking at the organizations, it is interesting to see how geographical clusters emerge. Chinese universities are at the top, US mostly on the right, Europe on the left, and industry right in the middle.

We can do the same for authors. The closeness in the graph reflects a combination of topic similarity and the frequency of collaboration.

Finally, we can do the same for countries. Given that all countries are working on a range of different topics, this graph is likely more representative of their collaboration frequency.

Additional Statistics

Finally, let's finish off with a couple of fun stats.

• Percentage of papers mentioning GitHub (indicating that the code is made available): ACL 70%, EMNLP 69%, NAACL 68%, ICLR 56%, NeurIPS 46%, ICML 45%, AAAI 31%. It seems the NLP papers are releasing their code much more freely.
• Percentage of papers mentioning MNIST: NeurIPS 20%, ICML 25%, ICLR 32%. Seems like it's still a cornerstone of ML research.
• Most authors on a single paper: 24. CoSQL: A Conversational Text-to-SQL Challenge Towards Cross-Domain Natural Language Interfaces to Databases
• The longest paper title: What if We Simply Swap the Two Text Fragments? A Straightforward yet Effective Way to Test the Robustness of Methods to Confounding Signals in Nature Language Inference Tasks
• The shortest paper title: Graph U-Nets

That's it for this time. Looking forward to all the interesting work that is going to be published in 2020!

The data used in this post can be found here.

The growth of interest in NLP technology, fuelled largely by investment in AI applications, has been accompanied by unprecedented expansion of the preeminent NLP conferences: ACL, NAACL and EMNLP in particular. Grzegorz Chrupała’s graph shows the rapid growth in submissions to each conference in recent years:

These trends can also be seen in the blog post by the ACL 2019 Chairs. Meanwhile, acceptance rates have tended to remain constant, meaning that the conferences have grown in line with submissions, e.g. from ACL 2019:

NLP has developed as a field narrowly focused on English, a point highlighted by the recent emergence (and need for) the #BenderRule. The ability of NLP models to deal with English is important, due to its status as an international language of politics, commerce and culture, and indeed with these tools we can handle, for instance, more than half the content on the internet. But with such a strong focus on English we miss cross-linguistic insights and lack coverage for the majority of languages in the world.

Staying on top of recent work is an important part of being a good researcher, but this can be quite difficult. Thousands of new papers are published every year at the main ML and NLP conferences, not to mention all the specialised workshops and everything that shows up on ArXiv. Going through all of them, even just to find the papers that you want to read in more depth, can be very time-consuming.

In this post, I have summarised 50 papers. After going through a paper, if I had the chance, I would write down a few notes and summarise the work in a couple of sentences. These are not meant as reviews – I’m not commenting on whether I think the paper is good or not. But I do try to present the crux of the paper as bluntly as possible, without unnecessary sales tactics. Hopefully this can give you the general idea of 50 papers, in roughly 20 minutes of reading time.

The papers are not selected or ordered based on any criteria. It is not a list of the best papers I have read, more like a random sample. The only filter that I applied was to exclude papers older than 2016, as the goal is to give an overview of the more recent work.

I set out to summarise 50 papers. Once I was done, I thought this would be a sensible place to summarise my own work as well. So at the end of the list you will also find brief summaries of the papers I published in 2017.

Let’s get started.

1. A Thorough Examination of the CNN/Daily Mail Reading Comprehension Task
Danqi Chen, Jason Bolton, Christopher D. Manning. Stanford. ACL 2016.
https://arxiv.org/pdf/1606.02858.pdf

Hermann et al (2015) created a dataset for testing reading comprehension by extracting summarised bullet points from CNN and Daily Mail. All the entities in the text are anonymised and the task is to place correct entities into empty slots based on the news article.

This paper has hand-reviewed 100 samples from the dataset and concludes that around 25% of the questions are difficult or impossible to answer even for a human, mostly due to the anonymisation process. They present a simple classifier that achieves unexpectedly good results, and a neural network based on attention that beats all previous results by quite a margin.

2. Word Translation Without Parallel Data
Alexis Conneau, Guillaume Lample, Marc’Aurelio Ranzato, Ludovic Denoyer, Hervé Jégou. Facebook, Le Mans, Sorbonne. ArXiv 2017.
https://arxiv.org/pdf/1710.04087.pdf

Inducing word translations using only monolingual corpora for two languages. Separate embeddings are trained for each language and a mapping is learned though an adversarial objective, along with an orthogonality constraint on the most frequent words. A strategy for an unsupervised stopping criterion is also proposed.